Suma y resta de vectores

Suma y resta de vectores mediante pares ordenados

Veamos como sumar o restar vectores cuando estos se encuentran expresados mediante pares ordenados o componentes.

Para sumar o restar dos o más vectores que se encuentran expresados mediante pares ordenados, solamente se tienen que sumar o restar las componentes rectangulares en los ejes “x” e “y” de forma independiente (valores en «x» e «y»). Veamos algunos ejemplos para que demostrar lo fácil que es sumar o restar vectores cuando estos se encuentran expresados mediante pares ordenados.

¿Qué representa el par ordenado?

Un vector expresado mediante un par ordenado (x; y) nos brinda las componentes del vector, y para graficarlo, debemos tener en cuenta que su cola se encontrará en el origen de coordenadas (0; 0) y el extremo de su cabeza en la ubicación (x; y).

Por ejemplo, si queremos graficar el vector Ā = (4; 3), su cola se encontrará en el origen de coordenadas (0; 0) y el extremo de su cabeza estará en la ubicación (4; 3).

Sumar o restar vectores mediante pares ordenados

Veamos ahora algunos ejemplos. A partir de los siguientes vectores:

• Ā = (2; 3)
  
• B̄ = (4; 1)
• C̄ = (3; 5)
• D̄ = (2; -3)

Ejemplo 1: calcular  Ā + B̄

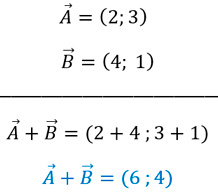
Ejemplo 2: calcular  C̄ + D̄

Ejemplo 3: calcular  B̄ – D̄

Ejemplo 4:

A partir de la gráfica, calcular Ē – Ḡ.

Solución:

Primero representamos cada vector mediante un par ordenado, y luego realizamos la resta como habíamos practicado en los ejemplos anteriores. 

Opcionalmente, aunque el problema no lo pide, podemos graficar Ē – Ḡ.

Guía de ejercicios

A continuación, viene una guía con muchos ejercicios de vectores, resolveremos algunos en el video que viene líneas abajo.

Vectores, ejercicios propuestos PDF.

-------------------------------------

👇

Ver más de sumas y restas poligonales 

👇