El método del triángulo es un método que permite hallar la suma o resultante de dos vectores. El método consiste en ubicar los vectores uno a continuación del otro, unidos mediante cabeza y cola. El vector resultante se obtiene uniendo la cola del primero con la cabeza del último.
En la siguiente gráfica, vamos a ver como sumar los vectores Ā y B̄ mediante el método del triángulo:

Ejemplo 1:
De manera gráfica, trazar el vector resultante de los vectores Ā y B̄.
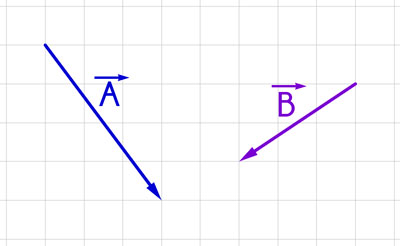
Solución:
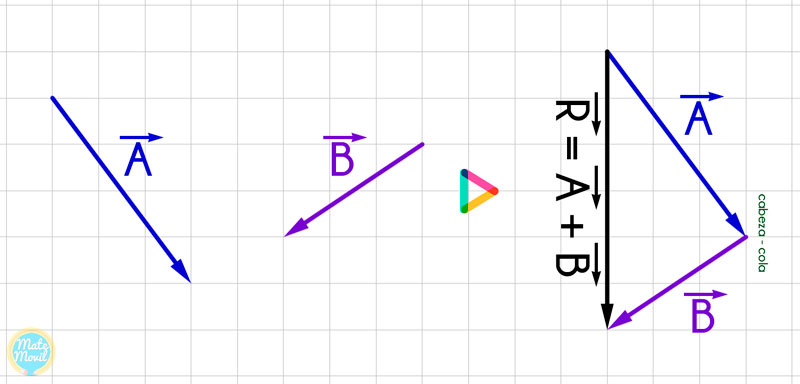
El vector resultante, es decir, el vector que resulta de sumar los vectores Ā y B̄, lo vamos a obtener mediante el método del triángulo. Por ello, vamos a trasladar los vectores Ā y B̄, de tal manera que los vectores Ā y B̄ se encuentren uno a continuación del otro, unidos mediante cabeza y cola.
El vector resultante, lo veremos de color negro, y se obtiene trazando un vector que parte de la cola del primero y termina en la cabeza del último.
Ejemplo 2:
Para el sistema de vectores mostrado, encontrar el vector resultante:
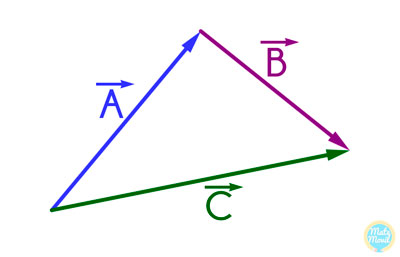
Solución:
En este ejercicio, tenemos que calcular el vector resultante, es decir, el vector que resulta de sumar los vectores Ā, B̄ y C̄:

En el gráfico, podemos ver que los vectores Ā y B̄, se encuentran uno a continuación del otro, unidos mediante cabeza y cola, por ello, podemos sumarlos usando el método del triángulo. El vector que resulta de sumar el vector Ā y el vector B̄, es el vector que parte de la cola de Ā y termina en la cabeza de B̄, y ese vector, es el vector C̄. Es decir, la suma del vector Ā con el vector B̄, es el vector C̄. Por lo tanto:

Guía de ejercicios
A continuación, viene una guía con muchísimos problemas propuestos de vectores, resolveremos algunos en el video.
------------------------------------------------------
Método del polígono (cabeza y cola), suma de vectores
Veamos algunos ejercicios resueltos y problemas propuestos del método del polígono para sumar vectores y encontrar el vector resultante.
El método del polígono, o también conocido como cabeza y cola, es un método que permite sumar vectores y consiste en colocar los vectores a sumar uno a continuación del otro, siempre la cabeza de un vector estará unida a la cola del siguiente; así, el vector resultante R̄ se traza uniendo la cola del primer vector con la cabeza del último vector.
Con este método, podemos sumar 2, 3 o más vectores. Recuerda que los vectores no son simples números, por ello, solo los podemos sumar empleando ciertos métodos, como el método del polígono.

En la siguiente gráfica, podemos ver los pasos para encontrar el vector resultante R̄.
Ejemplo 1:
Encontrar el módulo de la resultante de los vectores Ā, B̄ y C̄.

Solución:
Primero vamos a calcular el vector resultante R̄, luego calcularemos su módulo.
Aplicamos el método del polígono, colocando los vectores uno a continuación del otro, siempre unidos mediante cabeza y cola.

El vector resultante R̄, se traza uniendo la cola del primero con la cabeza del último.

Finalmente, calculamos el módulo del vector resultante, es decir, el tamaño o longitud de este vector.
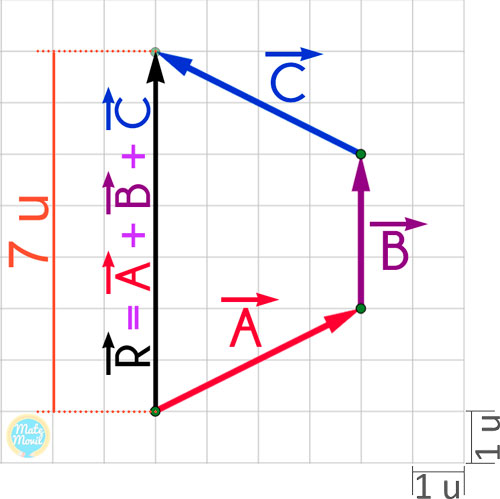
Finalmente, podemos ver que el módulo del vector resultante R̄, es de 7 u.

Caso Especial
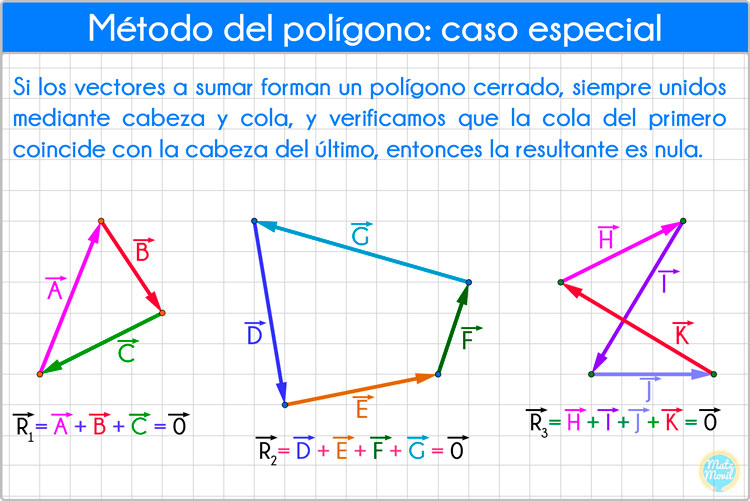
Si los vectores a sumar forman un polígono cerrado, siempre unidos mediante cabeza y cola, y verificamos que la cola del primero coincide con la cabeza del último, entonces la resultante es nula.
Ejemplo 2:
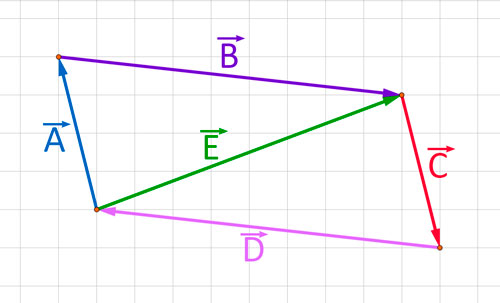
Encontrar la resultante de los vectores Ā, B̄, C̄, D̄ y Ē.
Solución:
En este problema nos piden encontrar la resultante de los 5 vectores de la gráfica:

Aplicamos el método del polígono solamente con los vectores Ā, B̄, C̄ y D̄, estos se encuentran uno a continuación del otro, siempre unidos mediante cabeza y cola. El vector resultante o suma de estos 4 vectores, se traza uniendo la cola del primero con la cabeza del último. Pero en este problema, sucede algo muy interesante, pues nuestros 4 vectores, cuando son ubicados uno a continuación del otro, unidos siempre mediante cabeza y cola, forman un polígono cerrado, y además, verificamos que la cabeza del último coincide con la cola del primero.

Por esas razones, nos encontramos ante el caso especial del método del polígono, y sabemos que la suma de estos 4 vectores es nula.

Finalmente, solo nos queda encontrar la resultante de los 5 vectores originales:

Guía de ejercicios
A continuación, viene una guía con muchísimos ejercicios de vectores, resolveremos algunos cuantos en el video que viene líneas abajo.

No hay comentarios.:
Publicar un comentario