FUNCION CONSTANTE

Función constante, ejercicios resueltos

La función constante es aquella función que toma el mismo valor de f(x) para cualquier valor de x. En otras palabras, sin importar el valor que toma x, f(x) siempre vale lo mismo. Hagamos un breve repaso de la teoría y luego veremos algunos ejercicios.

La función constante siempre tiene la forma:

Algunos ejemplos de función constante:

Gráfica de la función constante

La función constante siempre nos genera una recta horizontal. Por ejemplo, la gráfica de la función constante f(x) = +2 es la siguiente:

Dominio y rango de una función constante

Una función constante de la forma: f(x) = k; tiene el siguiente dominio y rango:

Dominio: x ∈ R
Rango: y = {k}

Pendiente de una función constante

Dado que la función constante siempre nos genera una recta horizontal, el ángulo de inclinación(α) es 0°, y el valor de la pendiente (m=tanα), es también 0. Si quieres conocer un poco más sobre el tema de pendientes, puedes visitar este artículo.

Video

A continuación, viene el video que hemos preparado, revisaremos primero la teoría y luego vienen los ejercicios.

FUNCION LINEAL

Funciones, introducción y ejercicios resueltos

Veamos la introducción, repaso y ejercicios resueltos de funciones matemáticas.

Una función es la regla que asigna a cada elemento del conjunto de partida, un solo elemento del conjunto de llegada.

El dominio es el conjunto de valores que toma la variable X, para los cuáles la función está definida. También se le conoce como conjunto de partida.

El contradominio es el conjunto de valores posibles para Y. También se llama conjunto de llegada.

El rango es el conjunto de valores del contradominio que son imágenes de X … y=f(x)

Es importante aclarar, que en muchas ocasiones el contradominio y rango son iguales, es por ello, que suelen crearse confusiones, sin embargo, no son lo mismo. Con el siguiente diagrama de flechas, los conceptos quedarán claros:

Gráfica

Pares ordenados

Tabla de valores

¿Cómo saber si una gráfica representa a una función?

Para saber si una gráfica representa a una función, hay que realizar la prueba de la recta vertical, la cual consiste en trazar diversas rectas verticales; y luego ver la cantidad de intersecciones. Si no hay rectas verticales intersecando a la curva en 2 o más puntos, entonces se trata de una función.

Recordemos que en una función, a cada elemento de «x» le corresponde un único elemento de «y». Ejemplos:

Evaluación de funciones, ejercicios resueltos

Veamos los problemas propuestos y ejercicios resueltos de evaluación de funciones en 3 niveles de dificultad.

Hasta ahora, habíamos revisado la definición de una función, habíamos visto la definición de una función, y también el conjunto de partida y el conjunto de llegada. En este capítulo, vamos a centrarnos en evaluar el valor que toma la función, de acuerdo al valor de la variable independiente, es decir, X.

Recuerda que en una función, tenemos siempre una variable independiente (X), y una variable dependiente (Y).

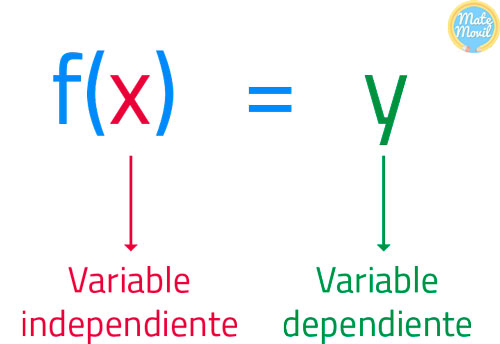
¿Cómo evaluar una función?

Para evaluar la función f en un número, sustituimos el número por X (variable independiente) en la definición de f.

Veamos el siguiente ejemplo:
Evaluar la función f en los siguientes valores: f(0) ; f(1) ; f(2); sabiendo que f (x)= x2 – 1

Como graficar funciones básicas

Luego de ver la introducción a funciones, hoy vamos a revisar como graficar funciones básicas. El método que veremos es muy sencillo, y consiste en 3 pasos que revisaremos líneas abajo. Al final de este artículo, encontrarás un video con la gráfica de diferentes funciones que hemos preparado para practicar.

Pasos para graficar funciones básicas

1. Arma una tabla de valores, tabulando diferentes valores de “x”, “y”, y colocando los pares ordenados. Hagamos el ejemplo de la función: y = 2x + 1

x	-2	-1	0	+1	+2
y	-3	-1	+1	+3	+5
(x;y)	(-2 ; -3)	(-1 ; +1)	(0 ; +1)	(+1 ; +3)	(+2 ; +5)

2. Coloca los pares ordenados en el plano cartesiano.

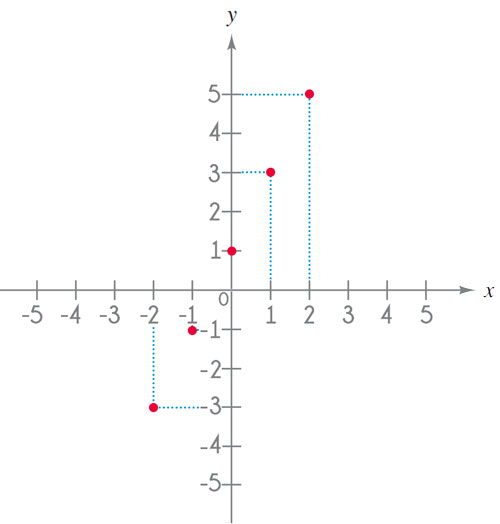
3. Une los puntos formando la curva.

Con estos pasos, puedes graficar cualquier función, ya sea lineal, cuadrática, exponencial, valor absoluto, entre otras. Más adelante, veremos otras funciones de mayor dificultad, analizando dominio, rango, intersecciones, paridad, asíntotas y más.

Acontinuación analizaremos algunos ejemplos de situaciones cotidianas que pueden ser interpretadas a través de funciones lineales

Situación 1: Un tércnico en reparaciones de electrodomésticos cobra $25 por la visita, más $20 por cada hora de trabajo ¿Qué función lineal expresa el dinero que debemos pagar en total, en relación al tiempo trabajado? ¿Cuál es

su representación gráfica?

Solución Observemos que en este problema x representa las horas de trabajo, mientras que f(x) el dinero total que cobra el técnico por hora de trabajo. La función lineal buscada es f(x) = 20x+25, cuya gráfica nos queda:

Situación 2:

Una compañía de teléfonos celulares tiene inicialmente 7 mil usuarios, y el número de éstos crere alrededor de 4 mil por año. ¿Cuál es la expresión de la función lineal que describe esta situación? ¿En qué año la empresa tendrá más de 15 mil usuarios?

Solución:

En esta sitaución x representa los años de la empresa, mientras que f(x) el número de usuarios (medido de miles) al cabo de los años transcurridos desde el inicio de la empresa.

La función lineal buscada es f(x) = 4x+7, cuya gráfica es:

FUNCION CUADRATICA

Función cuadrática, ejercicios resueltos

Continuamos con nuestro curso de Cálculo, y hoy vamos a revisar el capítulo de función cuadrática. Hemos preparado varios videos y muchos ejercicios resueltos de diferente tipo para estar listos para el examen. Empezamos con un breve repaso de la teoría.

Repaso

Función cuadrática o de segundo grado

Es una función de la forma ax2 + bx + c; donde a,b,c ∈ IR (reales) y a ≠ 0.

Ejemplos: determinar si las siguientes funciones son cuadráticas o de segundo grado.

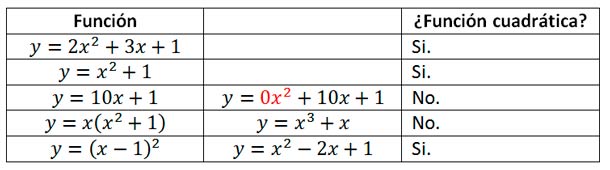
Formas de la función cuadrática

La función cuadrática se puede expresar de dos formas diferentes:

Siendo «h» y «k» los valores que nos darán la ubicación del vértice como veremos líneas abajo.

¿Cómo graficar una función cuadrática?

Cuando graficamos una función cuadrática, siempre obtenemos una parábola. Para graficar una función cuadrática, usamos a los siguientes puntos:

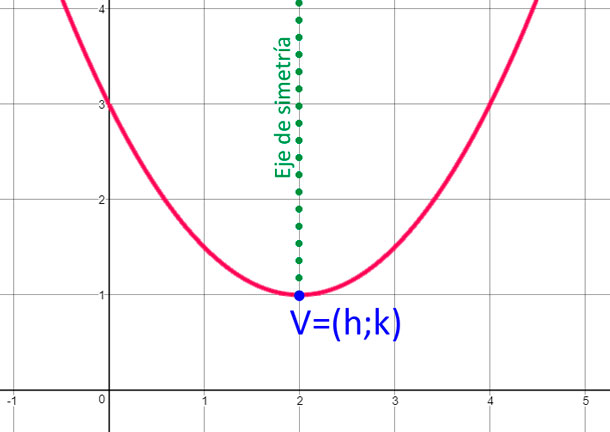
1 Vértice

El vértice de una parábola con coordenadas (h;k) se determina con las siguientes fórmulas:

2 Eje de simetría

Para encontrar la ecuación de la recta que define el eje de simetría, simplemente usamos esta fórmula:

3 Intersecciones con los ejes

Para encontrar la intersección de una función con el eje “x”, simplemente tenemos que realizar y = 0; y luego resolvemos la ecuación cuadrática que nos queda.

Para encontrar la intersección de una función con el eje “y”, simplemente tenemos que realizar x = 0; y luego resolvemos la ecuación que nos queda.

Función cuadrática, introducción

Veamos ahora el video de introducción a la función cuadrática con repaso de teoría y ejercicios resueltos sencillos.

Función cuadrática: forma canónica, vértice e intersecciones

Viene ahora los problemas de convertir una función cuadrática a la forma canónica.

Función cuadrática ejemplo

Representa gráficamente la función f cuya ecuación es f(x) = x^2 – 4x – 5.

Solución:

Como la función viene dada por una ecuación de la forma y = ax^2 +bx +c, para dibujar el gráfico:

1. Determinas las coordenadas del vértice:o Para hallar la abscisa del vértice utilizas la fórmula =

De la ecuación se obtiene que a = 1, b = – 4 y c = – 5.

= o La ordenada del vértice se calcula sustituyendo la obtenida en la ecuación.

= 2^2 – 4.2 – 5 = 4 – 8 – 5 = – 9

2. El vértice tiene coordenadas V(2 ; – 9).

3. Hallas los ceros:

Los ceros se determinan mediante la descomposición factorial.

x^2 – 4x – 5 = 0 (Igualas a cero la ecuación)

(x – 5)(x + 1) = 0 (Factorizas el trinomio)

x – 5 = 0 o x + 1= 0 (Igualas a cero cada factor)

x = 5 o x = – 1 (Despejas la x)

4. Hallas el intercepto con el eje "y":

Se halla sustituyendo en la ecuación la x por cero y realizando las operaciones indicadas.

y = 0^2 – 4.0 – 5 = – 5

Observa que cuando la ecuación está escrita en la forma y = ax^2 + bx + c, el intercepto coincide con el valor de c, por lo que no es necesario calcularlo.

Ahora, ubicas cada valor hallado en el sistema de coordenadas y trazas la parábola.