Varianza y desviación estándar, ejemplos y ejercicios

Veamos la varianza y la desviación estándar de la muestra y de la población, con ejercicios, ejemplos y veamos también las fórmulas.

La varianza y la desviación estándar son medidas de dispersión o variabilidad, es decir, indican la dispersión o separación de un conjunto de datos. Hay que tener en cuenta que las fórmulas de la varianza y la desviación estándar son diferentes para una muestra que para una población.

fórmulas de varianza y desviación estándar

Introducción

Varianza de la población (σ2)

La varianza se define como la media aritmética de los cuadrados de las diferencias de los datos con su media aritmética.

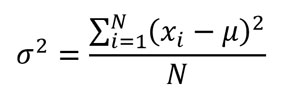
Desviación estándar de la población (σ)

La desviación estándar es la raíz cuadrada positiva de la varianza.

Te recomendamos calcular primero la varianza de la población y luego sacar su raíz cuadrada para obtener la desviación estándar.

Ten en cuenta que, si tienes una serie de valores de una población y necesitas calcular su varianza y su desviación estándar, deberás calcular primero la media poblacional µ con la siguiente fórmula:

Varianza de la muestra (s2)

La fórmula de la varianza de la muestra es diferente a la de varianza de la población.

Desviación estándar de la muestra (s)

Recuerda que la desviación estándar es la raíz cuadrada positiva de la varianza.

fórmula de la desviación estándar de la muestra

Te recomendamos calcular primero la varianza de la muestra y luego sacar su raíz cuadrada para obtener la desviación estándar.

Ten en cuenta que, si tienes una serie de valores de una muestra y necesitas calcular su varianza y su desviación estándar, deberás calcular primero la media poblacional x̄ con la siguiente fórmula:

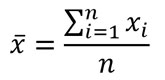
En los ejercicios, se siguen los siguientes pasos:

Se calcula la media.
Se calcula la varianza.
Se calcula la desviación estándar, que es la raíz cuadrada positiva de la varianza.

Ejemplo 1:

Calcular la varianza y la desviación estándar de los siguientes datos: 2, 4, 6 y 8 sabiendo que corresponden a una población.

Solución:Nos indican que estos datos forman una población, por lo tanto, usaremos las fórmulas de varianza y desviación estándar para la población, teniendo en cuenta que tenemos 4 datos, es decir, N = 4.

Empezamos calculando la media poblacional:

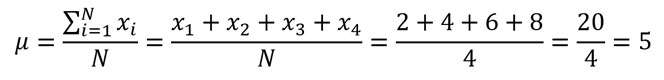
ejercicios de varianza y desviación estándar

Ahora calculamos la varianza poblacional:

El valor de la varianza poblacional, es de 5.

Ahora calculamos la desviación estándar, teniendo en cuenta que es la raíz cuadrada de la varianza.

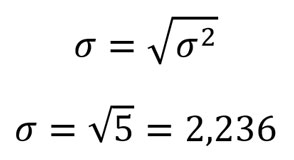
Ejemplo 2:

Calcular la varianza y la desviación estándar de los siguientes datos: 1, 3, 5, 7 y 9 sabiendo que corresponden a una muestra

Solución:Nos indican que estos datos forman una muestra, por lo tanto, usaremos las fórmulas de varianza y desviación estándar para la muestra, teniendo en cuenta que tenemos 5 datos, es decir, n = 5.

Empezamos calculando la media de la muestra:

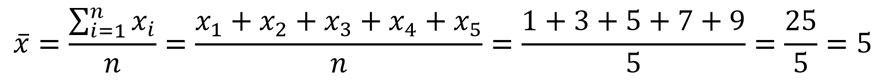
Ahora calculamos la varianza de la muestra:

El valor de la varianza poblacional, es de 10.

Ahora calculamos la desviación estándar, teniendo en cuenta que es la raíz cuadrada de la varianza.

Ejemplo 3:

Calcular la varianza y la desviación estándar de los siguientes datos: 10, 12, 13, 16, 9, 8, 12, 8, 6, 16 sabiendo que corresponden a una población.

Solución:

Empezaremos calculando la media y la varianza usando las fórmulas de la población.

En este caso, como tenemos muchos datos, recurriremos a una tabla para mantener el orden. Colocaremos los valores de los elementos de la población (xi) y sumaremos los valores.

ejercicios-de-varianza-y-desviación-estándar-111

Teniendo en cuenta que tenemos 10 datos (N = 10), calculamos la media:

Con el valor de la media, vamos en busca de la varianza poblacional:

ejercicios-de-varianza-y-desviación-estándar-3

Agregamos 2 columnas más a nuestra tabla para llegar a la forma de la varianza:

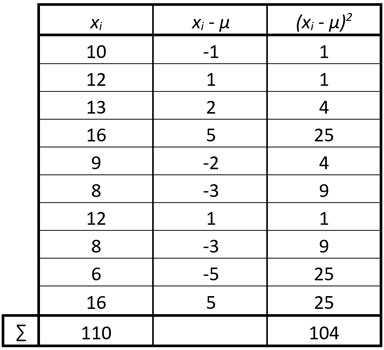
Reemplazamos los valores en la fórmula:

La varianza tiene un valor de 10,4.

Finalmente calculamos la desviación estándar:

La desviación estándar tiene un valor de 3,225.

-----------------------------------------------------------------------

Ejercicios y problemas de la varianza, desviación media y desviación típica

1Hallar la desviación media, la varianza y la desviación típica de la series de números siguientes:

a $2, 3, 6, 8, 11$ .

b $12, 6, 7, 3, 15, 10, 18, 5$ .

Solución:

aPara la serie de números $x_{1}=2, x_{2}=3, x_{3}=6, x_{4}=8, x_{5}=11$ con $n=5=N$ tenemos los siguientes cálculos.

Para la desviación media primero necesitamos calcular el valor de la media.

Media

$\displaystyle { \bar{x} = \frac{x_1+x_2+...+x_n}{n} }$

$\displaystyle { \bar{x} = \frac{2+3+6+8+11}{5} = 6 }$

Luego, calculamos el valor de la desviación media.

Desviación media

$\displaystyle{ D_{\bar{x}} = \frac{\mid x_1 - \bar{x} \mid + \mid x_2 - \bar{x} \mid +...+ \mid x_N - \bar{x} \mid}{N} }$

$\displaystyle{ D_{\bar{x}} = \frac{\mid 2 - 6 \mid + \mid 3 - 6 \mid +\mid 6 - 6 \mid + \mid 8-6 \mid + \mid 11-6 \mid}{5}= \frac{14}{5} = 2.8 }$

Ahora, calculamos el valor de la varianza.

Varianza

$\displaystyle{\sigma^2=\frac{(x_1-\bar{x})^2+(x_2-\bar{x})^2+...+(x_n-\bar{x})^2}{N} \qquad \mbox{\'o} \qquad \sigma^2=\frac{x_1^2+x_2^2+...+x_n^2}{N}-\bar{x}^2 }$

$\displaystyle{ \sigma^2=\frac{(2-6)^2+(3-6)^2+(6-6)^2+(8-6)^2+(11-6)^2}{5} = \frac{54}{5}= 10.8 }$

Y finalmente, calculamos el valor de la desviación típica.

Desviación típica

$\displaystyle{\sigma=\sqrt{\frac{(x_1-\bar{x})^2+(x_2-\bar{x})^2+...+(x_n-\bar{x})^2}{N}} }$

$\displaystyle{ \sigma = \sqrt{10.8} = 3.28 }$

bPara la serie de números $x_{1}=12, x_{2}=6, x_{3}=7, x_{4}=3, x_{5}=15, x_{6}=10, x_{7}=18, x_{8}=5$ con $n=8=N$ tenemos los siguientes cálculos.

Para la desviación media primero necesitamos calcular el valor de la media.

Media

$\displaystyle { \bar{x} = \frac{x_1+x_2+...+x_n}{n} }$

$\displaystyle { \bar{x} = \frac{12 + 6 + 7 + 3 + 15 + 10 + 18 + 5}{8} = \frac{76}{8}=9.5 }$

Luego, calculamos el valor de la desviación media.

Desviación media

$\displaystyle { D_{\bar{x}} = \frac{\mid x_1 - \bar{x} \mid + \mid x_2 - \bar{x} \mid +...+ \mid x_N - \bar{x} \mid}{N} }$

$\displaystyle { D_{\bar{x}} = \frac{\mid 12 - 9.5 \mid + \mid 6 - 9.5 \mid +\mid 7 - 9.5 \mid + \mid 3-9.5 \mid + \mid 15-9.5 \mid + \mid 10-9.5 \mid + \mid 18-9.5 \mid + \mid 5-9.5 \mid}{8}= \frac{32}{8} = 4 }$

Ahora, calculamos el valor de la varianza.

Varianza

$\displaystyle {\sigma^2=\frac{(x_1-\bar{x})^2+(x_2-\bar{x})^2+...+(x_n-\bar{x})^2}{N} \qquad \mbox{\'o} \qquad \sigma^2=\frac{x_1^2+x_2^2+...+x_n^2}{N}-\bar{x}^2 }$

$\displaystyle { \sigma^2 = \frac{12^2+6^2+7^2+3^2+15^2+10^2+18^2+5^2}{8}-9.5^2 = 23.75 }$

Y finalmente, calculamos el valor de la desviación típica.

Desviación típica

$\displaystyle {\sigma=\sqrt{\frac{(x_1-\bar{x})^2+(x_2-\bar{x})^2+...+(x_n-\bar{x})^2}{N}} }$

$\displaystyle { \sigma = \sqrt{23.75} = 4.87}$

2Un pediatra obtuvo la siguiente tabla sobre los meses de edad de 50 niños de su consulta en el momento de andar por primera vez. Calcular la varianza.

Meses	Niños
9	1
10	4
11	9
12	16
13	11
14	8
15	1

Solución:

Completamos la tabla con:

1 El producto de la variable por su frecuencia absoluta (xi · fi) para calcular la media.

2 El producto de la variable al cuadrado por su frecuencia absoluta (xi² · fi) para calcular la varianza y la desviación típica.

xi	fi	xi · fi	x²i · fi
9	1	9	81
10	4	40	400
11	9	99	1089
12	16	192	2304
13	11	143	1859
14	8	112	1568
15	1	15	225
	50	610	7526

Media aritmética

$\displaystyle {\bar{x}=\frac{610}{50} = 12.2}$

Varianza

$\displaystyle {\sigma^2=\frac{7526}{50} - 12.2^2 = 12.68}$

3El resultado de lanzar dos dados 120 veces viene dado por la tabla. Calcular la varianza.

Sumas	Veces
2	3
3	8
4	9
5	11
6	20
7	19
8	16
9	13
10	11
11	6
12	4

Solución:

Agregamos las columnas de xi · fi y de xi² · fi

xi	fi	xi · fi	xi² · fi
2	3	6	12
3	8	24	72
4	9	36	144
5	11	55	275
6	20	120	720
7	19	133	931
8	16	128	1024
9	13	117	1053
10	11	110	1100
11	6	66	726
12	4	48	576
	120	843	6633

Media aritmética

$\displaystyle {\bar{x}=\frac{843}{120} = 7.025}$

Varianza

$\displaystyle {\sigma^2=\frac{6633}{120} - 7.025^2 = 5.92}$

4Calcular la varianza de una distribución estadística que viene dada por la siguiente tabla.

	fi
[10, 15)	3
[15, 20)	5
[20, 25)	7
[25, 30)	4
[30, 35)	2

Solución:

Agregamos las columnas de xi · fi y de xi² · fi

	xi	fi	xi · fi	xi² · fi
[10, 15)	12.5	3	37.5	468.75
[15, 20)	17.5	5	87.5	1531.25
[20, 25)	22.5	7	157.5	3543.75
[25, 30)	27.5	4	110	3025
[30, 35)	32.5	2	65	2112.5
		21	457.5	10681.25

Solución:

Media

$\displaystyle {\bar{x} = \frac{457.5}{21} = 21.79}$

Varianza

$\displaystyle {\sigma^2=\frac{10681.25}{21} - 21.79^2=33.83 }$

5Calcular la varianza de la distribución de la tabla.

	xi	fi	xi · fi	xi² · fi
[10, 20)	15	1	15	225
[20, 30)	25	8	200	5000
[30,40)	35	10	350	12 250
[40, 50)	45	9	405	18 225
[50, 60)	55	8	440	24 200
[60,70)	65	4	260	16 900
[70, 80)	75	2	150	11 250
		42	1 820	88 050

Solución:

Media

$\displaystyle {\bar{x} = \frac{1820}{42} = 43.33}$

Varianza

$\displaystyle {\sigma^2=\frac{88050}{42} - 43.33^2=218.94 }$

6Las alturas de los jugadores de un equipo de baloncesto vienen dadas por la tabla. Calcula la varianza.

Altura	Nº de Jugadores
[1.70, 1.75)	1
[1.75, 1.80)	3
[1.80, 1.85)	4
[1.85, 1.90)	8
[1.90, 1.95)	5
[1.95, 2.00)	2

Solución:

Completamos la tabla con las columnas de xi · fi y de xi² · fi

	xi	fi	Fi	xi · fi	xi² · fi
[1.70, 1.75)	1.725	1	1	1.725	2.976
[1.75, 1.80)	1.775	3	4	5.325	9.452
[1.80, 1.85)	1.825	4	8	7.3	13.323
[1.85, 1.90)	1.875	8	16	15	28.125
[1.90, 1.95)	1.925	5	21	9.625	18.53
[1.95, 2.00)	1.975	2	23	3.95	7.802
		23		42.925	80.213

Media

$\displaystyle {\bar{x} = \frac{42.925}{23} = 1.866}$

Varianza

$\displaystyle {\sigma^2=\frac{80.213}{23} - 1.866^2=0.0056 }$

7Dada la distribución estadística. Calcular la varianza.

	fi
[0, 5)	3
[5, 10)	5
[10, 15)	7
[15, 20)	8
[20, 25)	2
[25, ∞)	6

	xi	fi	Fi
[0, 5)	2.5	3	3
[5, 10)	7.5	5	8
[10, 15)	12.5	7	15
[15, 20)	17.5	8	23
[20, 25)	22.5	2	25
[25, ∞)		6	31
		31

Solución:

Media

No se puede calcular la media, porque no se puede hallar la marca de clase del último intervalo.

Varianza

Si no hay media no es posible hallar la varianza.

8Considérese los siguientes datos: $3, 8, 4, 10, 6, 2$ . Se pide:

1 Calcular su media y su varianza.

2 Si los todos los datos anteriores los multiplicamos por $3$ , cúal será la nueva media y varianza.

xi	xi²
2	4
3	9
4	16
6	36
8	64
10	100
33	229

Solución:

1 Media y varianza:

Media

$\displaystyle {\bar{x} = \frac{33}{6} = 5.5}$

Varianza

$\displaystyl {\sigma^2=\frac{229}{6} - 5.5^2=7.92 }$

2Si todos los valores de la variable se multiplican por un número la media queda multiplicada por $3$ y la varianza queda multiplicada por el cuadrado de dicho número.

Media

$\displaystyle {\bar{x} = 5.5\cdot 3 = 16.5}$

Varianza

$\displaystyle {\sigma^2=7.92\cdot 3^2 = 71.28 }$

Profesor Ligdami

Analisis de varianza

Varianza y desviación estándar, ejemplos y ejercicios

Veamos la varianza y la desviación estándar de la muestra y de la población, con ejercicios, ejemplos y veamos también las fórmulas.

Introducción

Varianza de la población (σ2)

Desviación estándar de la población (σ)

Varianza de la muestra (s2)

Desviación estándar de la muestra (s)

Ejemplo 1:

Ejemplo 2:

Ejemplo 3:

Media

Desviación media

Varianza

Desviación típica

Media

Desviación media

Varianza

Desviación típica

Media aritmética

Varianza

Media aritmética

Varianza

Media

Varianza

Media

Varianza

Media

Varianza

Media

Varianza

Media

Varianza

Media

Varianza

No hay comentarios.: