Sucesiones Aritmética

Sucesión aritmética

Una sucesión es aritmética cuando cada término se obtiene sumando un número al término que le precede. Este número se denomina diferencia y se denota por $d$.

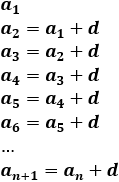
Ejemplo

La sucesión de los números pares es aritmética con diferencia $d=2$ ya que

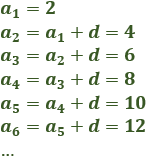
La diferencia se calcula restando dos términos consecutivos:

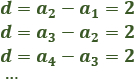
Fórmula para calcular la diferencia:

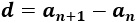
Es decir, la diferencia se obtiene restando términos consecutivos.

Si la diferencia entre dos términos consecutivos no es constante en toda la sucesión, entonces la sucesión no es aritmética.

TERMINO GENERAL

Se puede calcular cualquier término de la sucesión mediante una fórmula (fórmula o término general). Esta fórmula se obtiene a partir del primer término y de la diferencia:

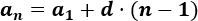
Ejemplo

Calculamos el término 10-ésimo de la sucesión de los pares.

Como el primer término es $a_1=2$ y la diferencia es $d=2$,

 el término que ocupa la décima posición es

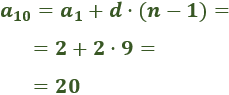
Suma de $n$ términos

Primera fórmula:

Conociendo el primer término y el término $n$-ésimo de la sucesión, podemos calcular la suma de los $n$ primeros términos con la fórmula

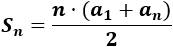
Ejemplo

Calculamos la suma de los 5 primeros términos de la sucesión de los pares.

Sin aplicar la fórmula:

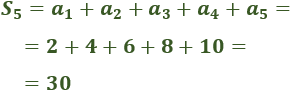
Aplicando la fórmula:

Como el primer término es $a_1=2$ y el quinto es $a_5=10$, la suma es

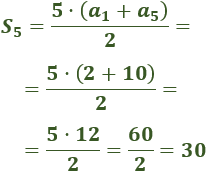
Segunda fórmula:

También podemos calcular la suma de los $n$ primeros términos a partir del primero y de la diferencia con la fórmula

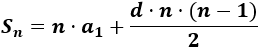
Ejemplo

Calculamos la suma de los 5 primeros términos de la sucesión de los pares:

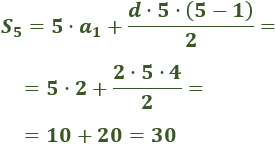
Bibliográfia 

Videos de sucesión aritmética 

Ejercisios de Sucesiones aritmética 

Problemas de progresiones y sucesiones 

Videos de ejemplos