Regls de 3 simple

La regla de tres es una de las formas para resolver problemas matemáticos de proporciones. Sirve para calcular un número desconocido con base en la relación entre dos cantidades o magnitudes.

La regla de tres se utiliza ordenando las cantidades conocidas separadas por dos puntos (:) colocando la cantidad conocida en el mismo lugar en relación a los dos puntos (:) donde está la cantidad o magnitud semejante; así por ejemplo si representamos por A y B a unas cantidades conocidas que tienen relación y queremos saber la relación cuando aumenta la cantidad representada por A, que representaremos por A’ se escribirá así:

A : B = A’ :  ?

Si el dato que conocemos es otra cantidad de B, que llamaremos B’, entonces se escribirá así:

A : B = ? : B’

Los datos así ordenados se identifican en relación al signo =, denominándolos centro a los más cercanos, y extremos a los alejados. Para calcular la incógnita, (o sea la cantidad desconocida), multiplicaremos los pares de datos conocidos, en relación al signo =, o sea, en el primer ejemplo los del centro y en el segundo ejemplo los de los extremos, y dividiremos el resultado entre  el dato conocido y del otro miembro de la ecuación.

Ejemplo de regla de tres:

Problema:

Si en seis minutos con 11 segundos he consumido 59 calorías, ¿Cuántas calorías consumiré en 10 minutos?

Paso 1

Primero ordenamos los datos y para facilitar las operaciones convertiremos los minutos a segundos:

Tiempo = 371 segundos

Calorías consumidas = 59 calorías

Tiempo 2 = 600 segundo

Calorías consumidas = X

Orden de los datos: 371 : 59 = 600 : X

Paso 2

Como conocemos las cantidades del centro (las más cercanas al signo =) las multiplicaremos:

59 x 600 = 35400

Paso tres

Ahora dividiremos el resultado obtenido entre el dato conocido:

35400 /  371 = 95.41778976

Por lo tanto en 10 minutos se consumirán 95.41778976

Otra forma de resolverlo:

Si ordenamos los mismos datos en forma distinta, también obtendremos el mismo resultado:

59 : 371 = X : 600

En este caso multiplicaremos los extremos y dividiremos entre el dato conocido del centro.

59 x 600 = 35400

35400 /371 = 95.41778976

Regla de 3 simple directa

Empezaremos viendo cómo aplicarla en casos de proporcionalidad directa (cuando aumenta una magnitud también lo hace la otra).

Colocaremos en una tabla los 3 datos (a los que llamamos “a”, “b” y “c”) y la incógnita, es decir, el dato que queremos averiguar (que llamaremos “x”). Después, aplicaremos la siguiente fórmula:

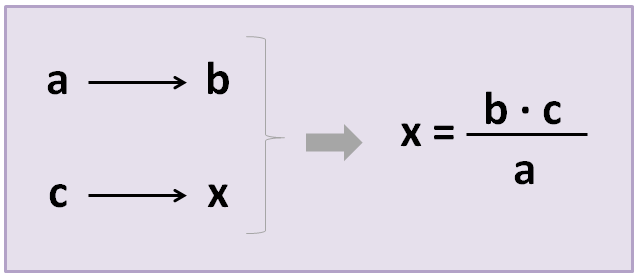
Para ver un ejemplo, vamos a resolver el mismo problema de proporcionalidad directa que vimos la semana pasada, ahora aplicando la regla de 3 simple.

Problema de regla de 3 simple directa

Al llegar al hotel nos han dado un mapa con los lugares de interés de la ciudad, y nos han dicho que 5 centímetros del mapa representan 600 metros de la realidad. Hoy queremos ir a un parque que se encuentra a 8 centímetros del hotel en el mapa. ¿A qué distancia del hotel se encuentra este parque?

Vamos a hacer la tabla con los 3 datos y la incógnita (“x”), y hallaremos “x” con la fórmula que acabamos de aprender:

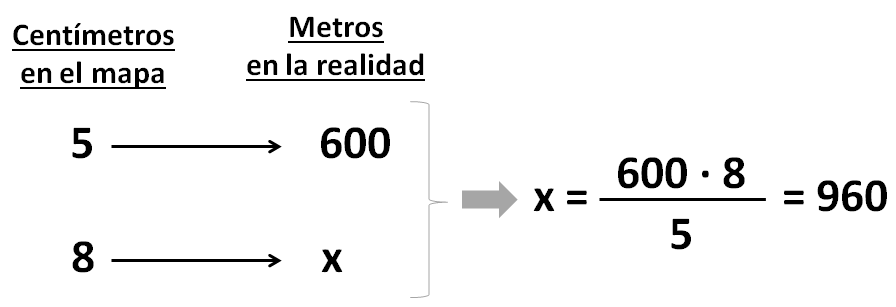
Solución: El parque se encuentra a 960 metros del hotel

Regla de 3 simple inversa

Ahora vamos a ver cómo aplicar la regla de 3 simple en casos de proporcionalidad inversa (cuando aumenta una magnitud disminuye la otra).

Colocaremos los 3 datos y la incógnita en la tabla igual que los hemos colocado en el caso anterior. Pero aplicaremos una fórmula distinta:

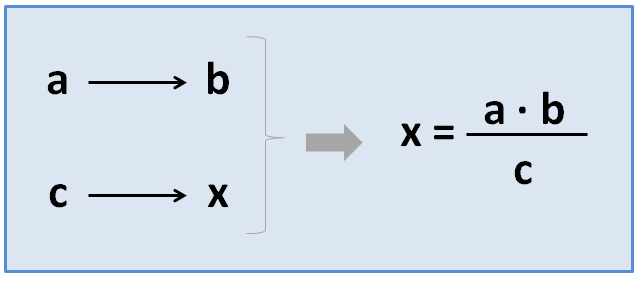
Problema de regla de 3 simple inversa

Vamos a ver un ejemplo con el mismo problema que resolvimos en el post de la semana anterior.

Ayer 2 camiones transportaron una mercancía desde el puerto hasta el almacén. Hoy 3 camiones, iguales a los de ayer, tendrán que hacer 6 viajes para transportar la misma cantidad de mercancía del almacén al centro comercial. ¿Cuántos viajes tuvieron que hacer ayer los camiones?

Colocamos los datos en una tabla y aplicamos la fórmula de la regla de 3 simple inversa:

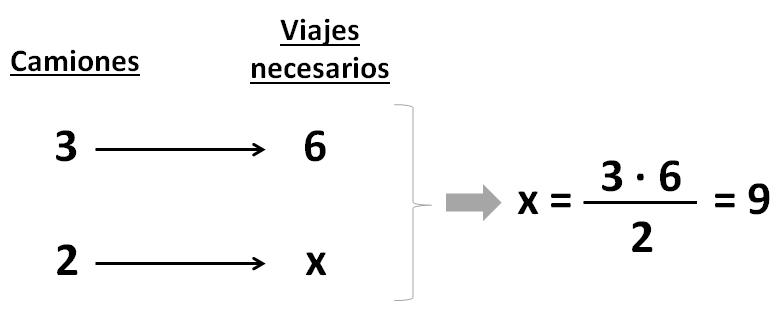
Solución: Ayer los 2 camiones hicieron 9 viajes.