Regla de tres compuesta

 Una Regla de Tres es una herramienta matemática que permite conocer un dato que guarda proporcionalidad con otros ofrecidos en el problema. Cuando se trata de una Regla de Tres Simple, sólo se abarcan dos magnitudes diferentes, con sus respectivos valores inicial y final, dando como resultado cuatro datos: tres para trabajo y uno como incógnita.

En el caso de una Regla de Tres Compuesta, hay más de dos magnitudes en el problema, pero sigue habiendo un único dato desconocido.

El procedimiento general para su solución consiste en lo siguiente:

En primer lugar, se requiere ordenar los datos en una tabla.

Segundo, hay que definir qué tipo de proporcionalidad conecta a los datos.

Puede tratarse de Proporcionalidad Directa, si el aumento o disminución de un valor corresponde al mismo cambio en la otra magnitud. Por otro lado, puede haber Proporcionalidad Inversa, si cuando una magnitud se incrementa o reduce, la otra sufre un cambio contrario.

Después, se establece la relación proporcional entre todos los datos, para proceder a calcular el elemento faltante.

De acuerdo con el tipo de Proporción que tengan los datos, la Regla de Tres Compuesta a aplicar va a adquirir un nombre: Regla de Tres Compuesta Directa si todas las magnitudes se comportan con proporción directa; Regla de Tres Compuesta Inversa si todas las magnitudes se comportan con una proporción inversa; y Regla de Tres Compuesta Mixta, cuando entre las magnitudes se presentan ambos tipos de Proporcionalidad. A continuación se citarán ejemplos de cada tipo de Regla de Tres Compuesta.

Regla de Tres Compuesta Directa 

La Relación de Proporcionalidad Directa se escribe de acuerdo con la siguiente expresión:

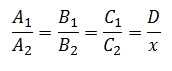
Ejemplo 1 

8 válvulas abiertas por 10 horas diarias han arrojado una cantidad de agua, con un valor de 400 pesos. Se requiere conocer el Precio del Vertido de 16 válvulas abiertas 12 horas durante los mismos días.

Fijando la variable de referencia, que es el Precio del Vertido, se analizan las Proporciones de las otras magnitudes con respecto a ella:

Mientras Mayor es el Número de Válvulas, Mayor es el Precio de Vertido. Proporción Directa.

Mientras Mayor es el Número de Horas diarias, Mayor es el Precio de Vertido. Proporción Directa.

Después se organizarán los datos en una tabla:

8 válvulas	10 horas diarias	400 pesos
16 válvulas	12 horas diarias	X (dato desconocido)

Ya sabiendo que la Proporción es Directa, se procede a hacer el arreglo matemático para solución, multiplicando Directamente los elementos conocidos, e igualándolos a la relación de magnitudes en que se encuentra la incógnita:

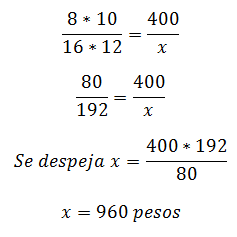
Ejemplo 2

Diez vendedores tienen ventas promedio de 400 artículos, con valor final de 30,000 pesos semanales. Se requiere estimar el valor de la venta para treinta y cinco vendedores con ventas promedio de 1500 artículos.

Mientras Mayor es el Número de Vendedores, Mayor es el Valor de la Venta. Proporcionalidad Directa.

Mientras Mayor es el Número de Artículos vendidos, Mayor es el Valor de la Venta. Proporcionalidad Directa.

Después se organizarán los datos en una tabla:

10 vendedores	400 artículos	$30,000
35 vendedores	1500 artículos	X (dato desconocido)

Ya sabiendo que la Proporción es Directa, se procede a hacer el arreglo matemático para solución, multiplicando Directamente los elementos conocidos, e igualándolos a la relación de magnitudes en que se encuentra la incógnita:

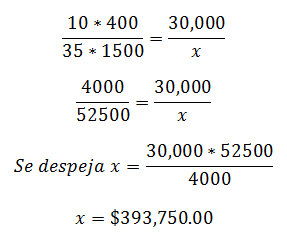
Regla de Tres Compuesta Inversa

La Relación de Proporcionalidad Inversa se escribe de acuerdo con la siguiente expresión:

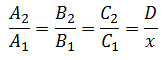
Ejemplo

4 Obreros trabajan 5 horas diarias construyendo un edificio en 2 días. Se necesita saber cuánto tardarán 3 obreros trabajando 6 horas diarias para construir un edificio idéntico.

Fijando la variable de los Días de Tardanza como referencia, se descubre el tipo de proporcionalidad entre los datos.

Mientras menos Obreros hay, Más días hay de tardanza. Proporcionalidad Inversa.

Mientras Más Horas Diarias de trabajo hay, menos días de tardanza. Proporcionalidad inversa.

Después, se organizarán los datos en una tabla:

4 Obreros	5 horas diarias	2 días de tardanza
3 Obreros	6 horas diarias	X (dato desconocido)

Y sabiendo que la Proporción es Indirecta en todos los casos, se procede a hacer el arreglo matemático para resolver la incógnita.

Regla de Tres Compuesta Mixta

La Relación de Proporcionalidad Mixta se puede escribir de acuerdo con la siguiente expresión:

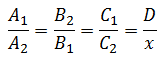
Ejemplo 

Si 8 obreros realizan en 9 días, trabajando a razón de 6 horas por día un muro de 30 metros, ¿cuántos días necesitarán 10 obreros trabajando 8 horas diarias para realizar otros 50 metros de muro que faltan?

Fijando la variable de referencia en los Días de Tardanza, se procede a analizar la proporcionalidad:

Mientras Más obreros, menos días de tardanza. Proporcionalidad Inversa.

Mientras Más horas, menos días de tardanza. Proporcionalidad Inversa.

Mientras Más metros de construcción, Más días de tardanza. Proporcionalidad Directa.

Después, se organizarán los datos en la tabla:

8 Obreros	9 días de tardanza	6 horas	30 metros
10 Obreros	X (dato desconocido)	8 horas	50 metros

Se procede a hacer el arreglo matemático para resolver la incógnita, tomando en cuenta la proporcionalidad en cada caso. Si la Proporcionalidad es Directa, se respeta la posición del número en la tabla para colocarlo en el numerador o denominador. Y cuando la Proporcionalidad es Inversa, se cambia su posición a la hora de multiplicar, al denominador o numerador, según sea el caso.