En esta pagina proporcionamos las reglas de derivacion y la regla de cadena y calculamos derivadas de funciones aplicando dichas reglas. Tambien, deducimos una regla o formula para derivar funciones del tipo
.
Contenido de esta pagina:
- Introduccion
- Reglas de derivacion
- Regla de la cadena
- Ejercicios resueltos (calculo de derivadas)
- Derivada de la funcion (ejercicio 16)
Regla de la cadena
La regla de la cadena nos proporciona la derivada de la composicion de funciones:
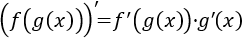
Es mas facil de entender mediante ejemplos.
Ejemplo 1:
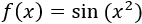
Se trata de la composicion de la funcion seno y la funcion cuadrado.
Su derivada es la derivada del seno por la derivada del cuadrado:
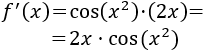
Ejemplo 2:
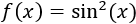
Tenemos las mismas funciones, pero con el orden de composicion intercambiado.
Su derivada es la derivada del cuadrado por la del seno:
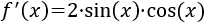
Basicamente, la regla de la cadena se puede resumir como "derivar y
multiplicar por la derivada de lo de dentro".
Ejemplo 3:
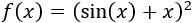
Para derivar esta funcion tenemos que aplicar la regla de la cadena
y la regla de derivacion de la suma de funciones:
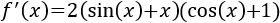
Ejemplo 1
Sea la función
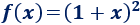
Es composición de las siguientes funciones:
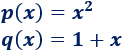
ya que
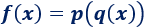
O, equivalentemente, .
Las derivadas son
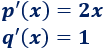
Por tanto, por la regla de la cadena,
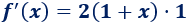
Ejemplo 2
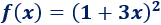
Aplicando la regla de la cadena, la derivada es la derivada
del cuadrado por la derivada del paréntesis:
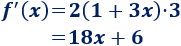
Ejemplo 3
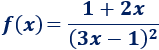
Tenemos que aplicar la regla del cociente y de la cadena
(para el cuadrado):
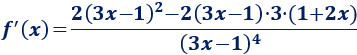
Simplificamos:
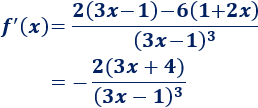
No hay comentarios.:
Publicar un comentario