Factorización
Antes de comenzar directamente con los casos de factoreo vamos a necesitar algunas definiciones:
Factor: Cuando un polinomio se escribe como producto de otros polinomios, cada polinomio del producto es un factor del polinomio original.
Factorización: es el proceso con el cual expresamos un polinomio como un producto.
Primo: Se dice que un polinomio es primo o irreducible cuando no puede escribirse como producto de dos polinomios de grado positivo.
Al factorizar un polinomio el objetivo es expresarlo como un producto de polinomios primos o potencias de polinomios primos, tratando principalmente de trabajar con los números enteros.
La factorización juega un papel importante en una gran cantidad de aplicaciones de la matemática, pues nos permite convertir expresiones muy complicadas en expresiones más simples facilitando así su estudio.
Para facturar un monomio se realiza por pura inspección, separando lo números y las letras entre si.
Prueba general de los factores
En cualquiera de los casos de factores la prueba es la misma multiplica los polinomios primos para ver si el resultado es el polinomio original
---------------------------------------------
Factor común
Se dice que un polinomio tiene factor común cuando una misma cantidad, ya sea número o letra, se encuentra en todos los términos del polinomio.
Si en todos los términos de un polinomio figura un factor común, dicho polinomio es igual al producto de ese factor por el polinomio que resulta al dividir cada término por ese factor.
Para efectuar el factor común hay que tomar en cuenta que este se realiza tanto para los números como para las letras, y con las letras se toma la que tenga el menor exponente de todas.
Ejemplo:
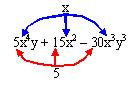
Como puede verse el cinco es el común numérico y la “x” la única letra común en este polinomio, como dos es el menor exponente de “x” es este el exponente que se tomara en cuenta, siendo el factor común 5x2.
Nos queda como respuesta:
Nos queda como respuesta:
Ejemplos:
Encontrar el factor común de los siguientes términos:
Encontrar el factor común de los siguientes términos:
--------------------------------------------------------
Factor común por agrupacion de terminos
Se llama factor común por agrupación de términos, si los términos de un polinomio pueden reunirse en grupos de términos con un factor común diferente en cada grupo.
Cuando pueden reunirse en grupos de igual número de términos se le saca en cada uno de ellos el factor común. Si queda la misma expresión en cada uno de los grupos entre paréntesis, se la saca este grupo como factor común, quedando así una multiplicación de polinomios.
Tratar desde el principio que nos queden iguales los términos de los paréntesis nos hará mas sencillo el resolver estos problemas.
2ax + 2bx - ay + 5a - by + 5b
Agrupo los términos que tienen un factor común:
(2ax - ay + 5a ) + ( 2bx - by + 5b )
Saco el factor común de cada grupo:
a ( 2x - y + 5 ) + b (2x - y + 5 )
Como las expresiones encerradas entre paréntesis son iguales se tiene:
( 2x -y +5 )(a + b)
Que es nuestra respuesta.
Ejemplos:
17ax – 17mx + 3ay - 3my + 7az – 7mz = a(17x +3y +7z) - m(17x + 3y +7z)
= (17x +3y +7z)(a – m)
= (17x +3y +7z)(a – m)
m(x + 2) – x – 2 + 3(x + 2) = (x + 2)(m + 3) -1(x + 2) = (x + 2)[(m + 3) – 1]
= (x + 2)(m + 3 – 1)
= (x + 2)(m + 3 – 1)
Otra forma de hacerlo:
m(x + 2) – x – 2 + 3(x + 2) = m(x + 2) -1(x + 2) + 3(x + 2) = (x + 2)(m + 3 -1)
--------------------------------------------------
Trinomio cuadrado perfecto
Se llama trinomio cuadrado perfecto al trinomio (polinomio de tres términos) tal que, dos de sus términos son cuadrados perfectos y el otro término es el doble producto de las bases de esos cuadrados.
En el trinomio cuadrado perfecto los términos cuadrados son siempre positivos, en cambio el término del doble producto puede ser negativo; en este caso debe ser negativo uno de los términos del binomio cuyo cuadrado es el trinomio dado, del ejemplo anterior tenemos:
Ambas son respuestas aceptables.
Regla para conocer si un trinomio es cuadrado perfecto.
Un trinomio ordenado con relación a una letra es cuadrado perfecto cuando la primera y tercer letra son cuadrados perfectos (o tienen raíz cuadrada exacta) y son positivos y el segundo termino es el doble producto de sus raíces cuadradas.
Ejemplos:
-------------------------------------------------------------
Trinomio cuadrado de la forma x2 + bx + c
Este tipo de trinomio tiene las siguientes características:
- Posee un termino que tiene la misma letra que el termino anterior pero elevada a 1 (bx) (puede ser negativo o positivo).
- Tienen un termino independiente de la letra que aparece en los otros dos (+ o -).
Reglas para factorizar un trinomio de esta forma:
- Se descompone el trinomio en dos factores binomios cuyo primer termino será la raíz cuadrada del termino
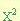 .
.
- El signo del primer binomio será el mismo signo que tenga el termino “bx”, el signo del segundo binomio será igual a la multiplicación de los signos de “bx” y de “c”.
- Si los dos factores tienen signos iguales entonces se buscan dos números cuya suma sea igual que el valor absoluto del factor “b” de “bx”, y cuyo producto sea igual al valor absoluto del factor “c”, estos números son los segundos términos de los factores binomios.
- Si los dos factores tienen signos diferentes entonces se buscan dos números cuya diferencia sea igual que el valor absoluto del factor “b” de “bx”, y cuyo producto sea igual al valor absoluto del factor “c”, el mayor de estos números será el segundo término del primer factor binomio, y el menor de estos números será el segundo término del segundo factor binomio.
Ejemplo explicativo:
Ejemplos:
Detengámonos un poco en los últimos dos ejemplos.
En el tercero podemos ver que lo que hemos llamado “x” no es una sola letra, pero aun así se utiliza el mismo procedimiento, esto es porque el “x” es un factor lo que implica que no necesariamente será una simple letra, este puede ser también un polinomio completo.
Siguiendo con el tercero vemos su cantidad numérica es bastante elevada y no todos pueden ver fácilmente los números que buscamos, una herramienta bastante útil es descomponer este numero en sus factores primos, de esta manera sabemos que cualquier combinación que hagamos al multiplicar estos números para formar los dos que busco cumplirán con el requisito multiplicativo y solo me preocupare por cumplir la suma algebraica. Así:
En el cuarto ejemplo se observa que el termino “c” no es un simple numero sino que tiene una forma 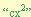 , en este caso no se ha hecho ninguna diferencia simplemente se a tomado como factor “b” como si fuera “21m” así al multiplicar (7m)(14m) nos resulta
, en este caso no se ha hecho ninguna diferencia simplemente se a tomado como factor “b” como si fuera “21m” así al multiplicar (7m)(14m) nos resulta 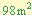 y al sumar 7m + 14m nos da 21m, con lo que se cumple con los requisitos.
y al sumar 7m + 14m nos da 21m, con lo que se cumple con los requisitos.
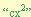 , en este caso no se ha hecho ninguna diferencia simplemente se a tomado como factor “b” como si fuera “21m” así al multiplicar (7m)(14m) nos resulta
, en este caso no se ha hecho ninguna diferencia simplemente se a tomado como factor “b” como si fuera “21m” así al multiplicar (7m)(14m) nos resulta 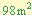 y al sumar 7m + 14m nos da 21m, con lo que se cumple con los requisitos.
y al sumar 7m + 14m nos da 21m, con lo que se cumple con los requisitos.
Los términos “x”, “b” y “c” pueden ser cualquier cosa, ya sea números, letras, o polinomios , solo se necesita que se cumplan las reglas indicadas
-------------------------------------------------------------
Trinomio cuadrado de la forma ax2 + bx + c
Este tipo de trinomio se diferencia del anterior debido a que el termino al cuadrado (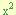 ) se encuentra precedido por un coeficiente diferente de uno (debe ser positivo). Este se trabaja de una manera un poco diferente, la cual detallamos a continuación:
) se encuentra precedido por un coeficiente diferente de uno (debe ser positivo). Este se trabaja de una manera un poco diferente, la cual detallamos a continuación:
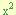 ) se encuentra precedido por un coeficiente diferente de uno (debe ser positivo). Este se trabaja de una manera un poco diferente, la cual detallamos a continuación:
) se encuentra precedido por un coeficiente diferente de uno (debe ser positivo). Este se trabaja de una manera un poco diferente, la cual detallamos a continuación:- Multiplicamos el coeficiente “a” de el factor “a
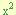 ” por cada termino del trinomio, dejando esta multiplicación indicada en el termino “bx” de la manera “b(ax)”, y en el termino “a
” por cada termino del trinomio, dejando esta multiplicación indicada en el termino “bx” de la manera “b(ax)”, y en el termino “a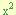 ” de la manera
” de la manera 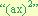 .
.
- Se descompone el trinomio en dos factores binomios cuyo primer termino será la raíz cuadrada del termino
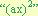 la que seria “ax”.
la que seria “ax”.
- al producto resultante lo dividimos entre el factor “a”, con el fin de no variar el valor del polinomio.
- El signo del primer binomio será el mismo signo que tenga el termino “bx”, el signo del segundo binomio será igual a la multiplicación de los signos de “bx” y de “c”.
- Se buscaran los segundos términos de los binomios según los pasos tres y cuatro del caso del trinomio anterior.
Ejemplo explicativo:
Ejemplos:
Siempre que sea posible hay que realizar la división indicada que nos queda de este tipo de trinomio, sin olvidar que cada factor del denominador que se simplifique se corresponde (2.3.5) a todos los términos de uno solo de los binomios
---------------------------------------------------------
Diferencia de cuadrados
La diferencia de cuadrados es una práctica que necesitamos tener clara para seguir avanzando en nuestro curso de Álgebra. Lo primero de todo es entender el concepto, saber qué significa la diferencia de cuadrados y cómo podemos ponerla en práctica. Por lo tanto, empecemos por el principio, la definición de diferencia de cuadrados.
Se le llama diferencia de cuadrados al binomio conformado por dos términos a los que se les puede sacar raíz cuadrada exacta.
Al estudiar los productos notables teníamos que:
En donde el resultado es una diferencia de cuadrados, para este capítulo es el caso contrario:
Donde siempre la diferencia de cuadrados es igual al producto de la suma por la diferencia de sus bases.
Pasos a seguir para calcula la diferencia de cuadrados:
- Se extrae la raíz cuadrada de ambos términos.
- Se multiplica la suma por la diferencia de estas cantidades (el segundo termino del binomio negativo es la raíz del termino del binomio que es negativo).
Factorización de una diferencia de cuadrados
La factorización de una diferencia de cuadrados está formada por una ecuación con dos términos: uno positivo y el otro, negativo. Ambos deben de ser raíces cuadradas exactas. Y lo que se hace es realizar una resta entre ellos. De ahí el nombre de factorización por diferencia de cuadrados.
Ejemplos de diferencias de cuadrados
¿Tienes claro ya qué es una diferencia de cuadrados? ¡Te dejamos aquí otros ejemplos para que lo tengas más claro!
Recuerda que tanto la diferencia de cuadrados como la factorización por diferencia de cuadrados te serán de gran utilidad para resolver problemas matemáticos y de álgebra en concreto. ¡No pases a la siguiente lección hasta que tengas claro este concepto! Solo así podrás ir aprendiendo paso a paso.
---------------------------------------------------------
Cubo perfecto de binomios (cuatrinomio)
De los productos notables tenemos:
En este caso la factorización es realizar la operación inversa a esta:
Para reconocerlo se deben tomar en cuenta los siguientes puntos:
- Debe tener cuatro términos, y estar ordenado con respecto a una letra.
- El segundo termino debe ser igual al triple producto del cuadrado de la raíz cúbica del primer termino por la raíz cúbica del cuarto termino [3(a)2(b)].
- El tercer termino debe ser igual al triple producto de la raíz cúbica del primer termino por el cuadrado la raíz cúbica del cuarto termino [3(a)(b)
 ].
].
- El segundo y el cuarto termino deben tener el mismo signo y puede ser positivo o negativo, el primer y tercer termino siempre son positivos (si el primer y tercer termino son negativos realizar factor común con el factor -1).
- Si todos los términos son positivos el resultado es el cubo de la suma de dos cantidades (a + b)
 , si hay términos negativos el resultado es el cubo de la diferencia de dos cantidades (a – b)
, si hay términos negativos el resultado es el cubo de la diferencia de dos cantidades (a – b) .
.
Ejemplo explicativo:
Ejemplos:
En este tipo de factoreo, se trata de reconocer que pertenece a este tipo polinomio
----------------------------------------------------------
Suma o diferencia de cubos perfectos
Recordamos de cocientes notables que:
Pero en la división exacta el dividendo es igual al divisor multiplicado por el cociente, efectuándolo nos queda:
De donde se deducen las siguientes reglas:
- La suma de dos cubos perfectos se descompone en dos factores, el primero es la suma de sus raíces cúbicas, y el segundo se compone de el cuadrado de la primera raíz menos el producto de ambas raíces más el cuadrado de la segunda raíz.
- La diferencia de dos cubos perfectos se descompone en dos factores, el primero es la diferencia de sus raíces cúbicas, y el segundo se compone del cuadrado de la primera raíz más el producto de ambas raíces mas el cuadrado de la segunda raíz.
Ejemplo explicativo:
Ejemplos:
--------------------------------------------------------
Pasos para factorizar la suma o diferencia de dos potencias iguales
Pasos:
- Clasificar la expresión en positiva o negativa, y en par o impar (si son positivas y pares no se pueden realizar por este método).
- Se sacan las raíces de cada termino.
- Se coloca el primer factor el cual es un binomio cuyo primer termino es la raíz del primer termino dado y el segundo termino es la raíz del segundo termino dado.
- El signo del primer factor (binomio) será el mismo que tiene la expresión dada.
- Se crea el segundo factor (un factor polinomio) en el cual existirá un número de términos igual al exponente de la expresión dada (los siguientes pasos son solo para el segundo factor).
- En cada término se multiplicara el término de la izquierda por el término de la derecha de la expresión dada
- En el primer término del factor polinomio el factor de la izquierda tendrá un exponente igual a “n – 1”, y el factor derecho tendrá un exponente de cero.
- Para los exponentes de los siguientes términos, en el caso del factor de la izquierda irán disminuyendo en una unidad, y los del termino de la derecha irán aumentando también en una unidad (si se suman los exponentes de los dos términos siempre será igual a n-1).
- Si el binomio es negativo todos los términos del polinomio son positivos, si el binomio es positivo impar los signos del polinomio se alternarán (+ ó –) comenzando por el “+”.
- Cuando en el polinomio, el exponente del termino de la derecha sea igual a n-1 damos por terminada la respuesta.
Ejemplos explicativos:
Al igual que en los demás casos un factor es cualquier cosa ya sea un numero una letra una combinación de números y letras y operaciones
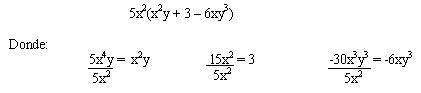
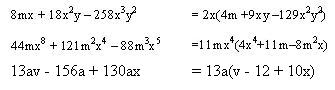

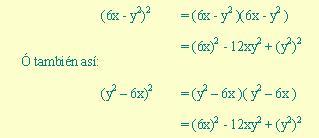
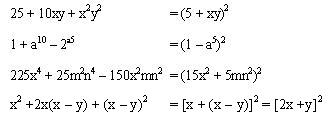
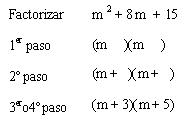
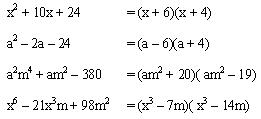



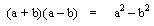
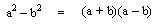
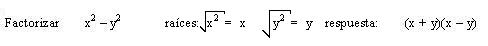
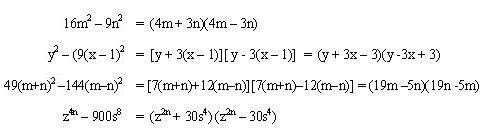
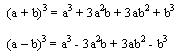
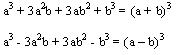


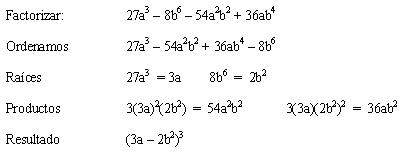
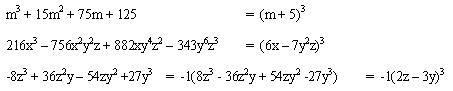
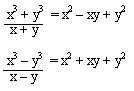
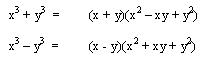
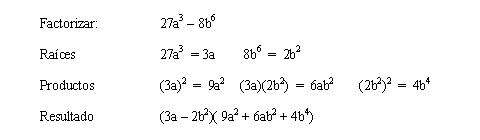
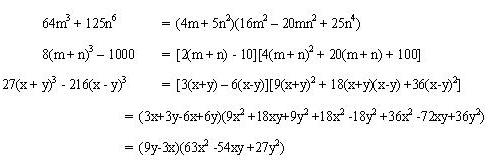

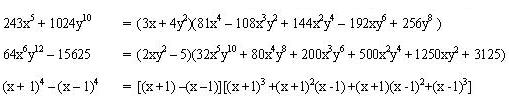
No hay comentarios.:
Publicar un comentario