¿Qué es la integración?
Integrar es el proceso recíproco de derivar, es decir, dada una función  , busca aquellas funciones
, busca aquellas funciones  que al ser derivadas conducen a
que al ser derivadas conducen a  .
.
 , busca aquellas funciones
, busca aquellas funciones  que al ser derivadas conducen a
que al ser derivadas conducen a  .
.
Se dice, entonces, que  es una primitiva o antiderivada de
es una primitiva o antiderivada de  ; dicho de otro modo las primitivas de
; dicho de otro modo las primitivas de  son las funciones derivables
son las funciones derivables  tales que:
tales que:
 es una primitiva o antiderivada de
es una primitiva o antiderivada de  ; dicho de otro modo las primitivas de
; dicho de otro modo las primitivas de  son las funciones derivables
son las funciones derivables  tales que:
tales que:
Si una función  tiene primitiva, tiene infinitas primitivas, diferenciándose todas ellas en una constante.
tiene primitiva, tiene infinitas primitivas, diferenciándose todas ellas en una constante.
 tiene primitiva, tiene infinitas primitivas, diferenciándose todas ellas en una constante.
tiene primitiva, tiene infinitas primitivas, diferenciándose todas ellas en una constante.![Rendered by QuickLaTeX.com \left [ F(x)+C \right ]'=F'(x)+0=F'(x)=f(x)](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-47fabb0fbac77756a92fac9425bba583_l3.png)
¿Qué es la integral indefinida?
La integral indefinida es el conjunto de las infinitas primitivas que puede tener una función.
- Se representa por
 .
. - Se lee : integral de
 de
de  diferencial de
diferencial de  .
.  es el signo de integración.
es el signo de integración. es el integrando o función a integrar.
es el integrando o función a integrar. es diferencial de
es diferencial de  , e indica cuál es la variable de la función que se integra.
, e indica cuál es la variable de la función que se integra. es la constante de integración y puede tomar cualquier valor numérico real.
es la constante de integración y puede tomar cualquier valor numérico real.- Si
 es una primitiva de
es una primitiva de  entonces:
entonces: 
- Para comprobar que la primitiva de una función es correcta basta con derivar.
Propiedades de la integral indefinida
1 La integral de una suma de funciones es igual a la suma de las integrales de esas funciones.
![Rendered by QuickLaTeX.com \int \left [ f(x)+g(x) \right ]dx= \int f(x)+ \int g(x)dx](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-90a5b1d51e6085ff93e97020e567e7c9_l3.png)
2 La integral del producto de una constante por una función es igual a la constante por la integral de la función.

Integrales Indefinidas
La idea de la integral indefinida supuso un paso más en el camino de la abstracción emprendido por las matemáticas modernas. Con ella, la integral dejó de referirse únicamente a un modo de determinar las áreas que forman curvas y rectas para asumir la condición de función en sí, susceptible de formar parte de ecuaciones y descripciones de modelos en el gran marco de las teorías del análisis matemático.
Primitivas
Dada una función f (x), se dice que la función F (x) es primitiva de ella si se verifica que F¿ (x) = f (x). La operación consistente en obtener la primitiva de una función dada se denomina integración, que es la inversa de la derivación.
De esta definición se desprende que la función f (x) posee infinitas primitivas, ya que si F (x) es primhtiva de f (x), también lo será cualquier otra función definida como G (x) = F (x) + C, siendo C un valor constante.
El conjunto de todas las primitivas de una función f (x) dada se denomina integral indefinida de la función, y se denota genéricamente como:
Las primitivas de una función forman una familia de curvas desplazadas verticalmente unas de otras. Así, la función f (x) = x tiene infinitas primitivas que difieren en una constante, tal como se muestra a la derecha.
Propiedades de las primitivas
Aplicando las propiedades de la derivación (ver t43), es posible determinar algunas propiedades comunes de la integración. Las siguientes propiedades de linealidadsirven para descomponer integrales complicadas en otras más sencillas:
- La integral de la suma (o diferencia) de dos funciones es igual a la suma (o diferencia) de las integrales de cada una de ellas.
- La integral del producto de una constante por una función es igual al producto de la constante por la integral de la función.
Tabla de integrales inmediatas
En la tabla siguiente se resumen las reglas de integración de algunas funciones comunes. En general, se llama integrales inmediatas a las que se deducen directamente de esta tabla y de las propiedades de linealidad de la integración.
Tabla de integrales inmediatas.
- Introducción
- Recordatorio: concepto de integral y propiedades
- 27 Integrales Inmediatas Resueltas
Páginas relacionadas:
- Integración por Partes
- Integración por Substitución
- Integración de Funciones Racionales
- Cálculo de Áreas
Introducción
Este es el nivel básico del cálculo de primitivas después de las integrales que se obtienen directamente a partir de la tabla de derivadas.
Las llamamos inmediatas ya que el método que usaremos consiste en, teniendo en cuenta las derivadas elementales (las de la tabla), conseguir en el integrando una función multiplicada por su derivada. De este modo, por la regla de la cadena, la primitiva es dicha función.
Por tanto, necesitamos conocer las derivadas elementales, las reglas de derivación y la regla de la cadena y las propiedades de las integrales
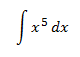
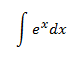
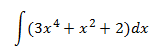
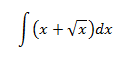
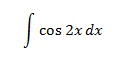
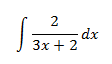
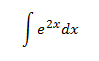
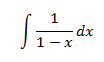
Las llamamos inmediatas ya que el método que usaremos consiste en, teniendo en cuenta las derivadas elementales (las de la tabla), conseguir en el integrando una función multiplicada por su derivada. De este modo, por la regla de la cadena, la primitiva es dicha función.
Por tanto, necesitamos conocer las derivadas elementales, las reglas de derivación y la regla de la cadena y las propiedades de las integrales
- Definición de primitiva:
Las primitivas de una función se representan por
Son el conjunto de funciones cuyas derivadas son iguales a . Es decir, es una primitiva de si .
Hablamos en plural ya que, por ejemplo, y son dos primitivas distintas de .Nótese que la diferencia entre ambas primitivas es sólo una constante. Por ello, cuando calculamos una integral, siempre escribimos la constante de integración :
El símbolo se denomina signo integral y indica que la variable de integración es .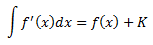
Ejemplos:
En la primera integral, tratamos la como una constante, integrando respecto de . En la segunda, es al contrario.
Propiedades de las integrales:- Integral de una Suma
Es decir, la integral de la suma de dos funciones es la suma de las integrales de ambas funciones.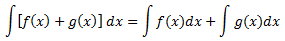
- Producto por una constante
Es decir, las constantes (números o parámetros; o factores que no sean función de x) salen fuera de la integral multiplicándola.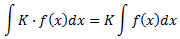
Esta propiedad será útil tanto de izquierda a derecha como de derecha a izquierda, pues en ocasiones necesitamos en el integrando un número en concreto para aplicar la regla de la cadena, por lo que multiplicaremos y dividiremos la integral por este número y, aplicando la propiedad, podemos introducir el factor que multiplica (o rl que divide) en el integrando.
- Ejemplo 1
Ejemplo 2
Ejemplo 3
Integrales resueltas
Integral 1
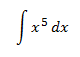
Solución
Integral 2
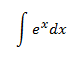
Solución
Integral 3
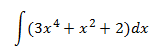
Solución
Integral 4
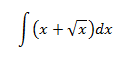
Solución
Integral 5
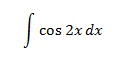
Solución
Integral 6
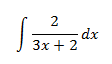
Solución
Integral 7
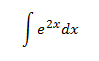
Solución
Integral 8
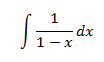
Solución
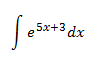
No hay comentarios.:
Publicar un comentario