La progresión geométrica es como se le llama al proceso en el que se consigue obtener una serie de números que son obtenidos mediante la multiplicación sucesiva utilizando un número que es denominado razón
Así la progresión geométrica es como se le conoce al conjunto de números, en los que dependiendo del primero los demás se obtienen multiplicando por un mismo número en forma constante para obtener el siguiente número.
La notación es como sigue:
a = al primer término
r = razón común
s = suma
n = número de términos
Una sucesión geométrica (o progresión geométrica) es una sucesión en la que cada término an se obtiene multiplicando al término anterior an-1 por un número r llamado razón.
Ejemplos:
- La sucesión 2, 4, 8, 16, 32,… es geométrica con razón r = 2:
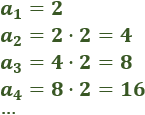
- La sucesión 1, -3, 9, -27, 81,… es geométrica con razón r = -3.
Razón
La razón se calcula dividiendo términos consecutivos:
Ejemplo:
Calculamos la razón de la siguiente sucesión geométrica:
Dividimos el segundo término entre el primero:
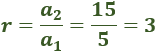
Comprobamos que la razón es constante:
Término general
El término general de una sucesión geométrica se calcula a partir del primer término a1 y de la razón r:
![]()
El término general permite calcular cualquier término de la sucesión sin necesidad de calcular los anteriores.
Ejemplo:
Calculamos el término general de la siguiente progresión geométrica:
La razón de la sucesión es r=3 ya que
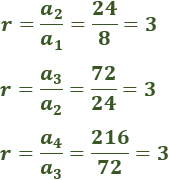
El término general de la sucesión es
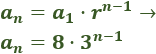
Suma de términos
Para sumar los primeros n términos de una progresión geométrica disponemos de varias fórmulas:
Primera fórmula:
Segunda fórmula:
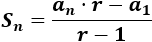
Nota: la segunda fórmula se ha calculado utilizando la fórmula del término general en la primera fórmula de la suma.
Suma de todos los términos
Cuando la razón de la progresión es |r|<1 se pueden sumar todos los términos mediante la fórmula
Bibliográfia
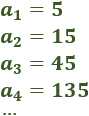
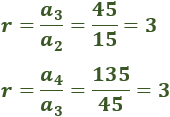
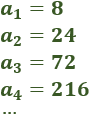
No hay comentarios.:
Publicar un comentario