Potenciacion

Potencias

Índice de Contenidos

• 1 Qué es una potencia
• 2 Potencias con base negativa
• 3 Propiedades de las Potencias
  • 3.1 Potencias con exponente uno
  • 3.2 Potencias con exponente cero
  • 3.3 Multiplicación de potencias con la misma base
  • 3.4 División de potencias con la misma base
  • 3.5 Multiplicación elevada a una potencia
  • 3.6 Cociente elevado a una potencia
  • 3.7 Potencia de otra potencia
  • 3.8 Potencias con exponente negativo
  • 3.9 Potencia de exponente racional
  • 3.10 Potencia de exponente racional y negativo
  • ---------------------------------------------------

Primero calculamos potencias aplicando la definición de la operación de potenciación, después explicaremos y aplicaremos las siguientes propiedades de las potencias:

Enlace: Ejercicios interactivos (operaciones con enteros)

---

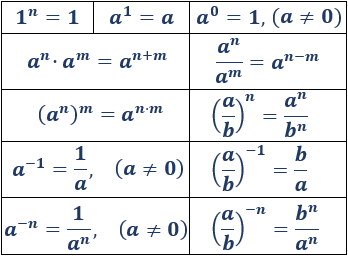
Definición

La potencia $a^n$ representa el producto que tiene $n$ veces el número $a$. El número $a$ se llama base y el número $n$ se llama exponente.

Ejemplo: potencias de 2:

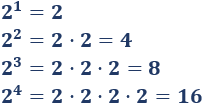
Problema 1

Calcular las potencias $3^2$, $5^3$, ${11}^1$, $7^0$, $1^{22}$, $6^2$ y $0^{20}$.

Solución

Por lo que hemos visto, podemos decir:

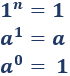
Dicho en palabras,

• Si la base de una potencia es 1, el resultado es 1.
• Si el exponente de una potencia es 1, el resultado es la base.
• Si el exponente de una potencia es 0 (y la base no es 0), el resultado es 1.

Problema 2

Calcular las siguientes potencias de números negativos: $(-1{)}^2$, $(-2{)}^3$, $(-5{)}^2$ y $(-1{)}^5$.
Ayuda: utilizar la regla de los signos (el producto de números con el mismo signo es un número positivo y el producto de números con signos distintos es un número negativo).

Solución

Observad que si la base de una potencia es negativa:

• El resultado es positivo si el exponente es par.
• El resultado es negativo si el exponente es impar.

Esto puede resumirse como:

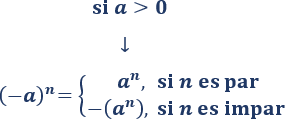
Problema 3

Comprobar que $(-3{)}^3=-(3^3)$ y que $(-5{)}^2=5^2$.

Solución

Exponente negativo

La potencia de un número distinto de 0 elevado a -1 es igual a su inverso:

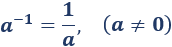
La potencia de un número distinto de 0 elevado al número negativo $-n$ es el inverso del número elevado a $n$:

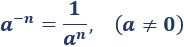
Problema 4

Calcular las siguientes potencias con exponente negativo: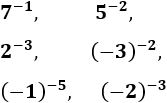

Solución

Producto y cociente de potencias

El producto de dos potencias con la misma base es la potencia de dicha base y cuyo exponente es la suma de los exponentes:

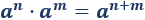
El cociente de dos potencias con la misma base es la potencia de dicha base y cuyo exponente es la resta de los exponentes:

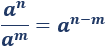
Problema 5

Calcular los siguientes productos de potencias: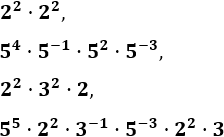

Solución

Problema 6

Calcular los siguientes cocientes de potencias: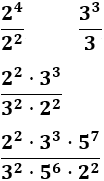

Solución

Potencia de una potencia

La potencia de una potencia con base $a$ es la potencia con base $a$ y cuyo exponente es el producto de los exponentes:

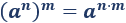
Problema 7

Calcula las siguientes potencias de potencias: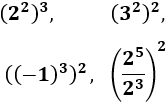

Solución

Potencia del producto y del cociente

La potencia de un producto de factores es igual al producto de las potencias de los factores:

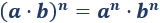
La potencia de un cociente de números es igual al cociente de las potencias de los números:

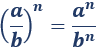
Problema 8

Calcular las siguientes potencias de fracciones: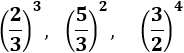

Solución

Potencia de una fracción con exponente negativo

El resultado de elevar una fracción a -1 es la fracción inversa (intercambiar el numerador y el denominador):

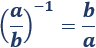
La potencia de una fracción con exponente negativo $-n$ es la potencia del inverso de la fracción con exponente $n$:

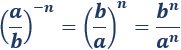
Problema 9

Calcular las siguientes potencias cuyos exponentes son negativos: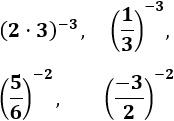

Solución

Problema 10

Escribir los siguientes números como productos de potencias cuyas bases sean números primos: 56, 60 y 90.

Solución

Las propiedades de las potencias nos permiten simplificar operaciones.

Problema 11

Simplificar la siguiente operación entre potencias escribiendo las bases como productos de números primos: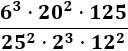

Solución