Multiplicación de un vector por un escalar
Veamos como multiplicar un vector por un escalar.
Hoy vamos a revisar que ocurre cuando multiplicamos un vector por un escalar (número real).
Si tenemos un vector Ā y una cantidad escalar k (un número real), entonces k·Ā es un vector paralelo al vector Ā, donde el sentido depende del signo de k. Aquí algunos ejemplos:
Veamos por aquí un ejemplo diferente:
En estos ejemplos, podemos apreciar lo siguiente:
- Si k es positivo, entonces los vectores Ā y k·Ā son paralelos y tienen la misma dirección.
- Si k es negativo, entonces los vectores Ā y k·Ā son paralelos y tienen direcciones opuestas.
Respecto al módulo del vector k·Ā, es decir, el tamaño o longitud del vector, este se obtiene mediante:
Ejemplo 1:
A partir del gráfico de Ā, graficar 3·Ā y -3·Ā.
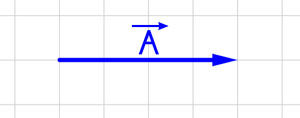
Solución:
Debemos tener en cuenta que el vector 3·Ā , tiene un módulo del triple del módulo del vector Ā y la misma dirección de este. Por otro lado, el vector -3·Ā , tiene un módulo del triple del módulo del vector Ā y dirección opuesta a este. Veamos la gráfica:
Multiplicación de un vector expresado mediante un par ordenado por un escalar
Si es que el vector Ā, se encuentra expresado mediante un par ordenado y lo multiplicamos por el escalar k, entonces obtenemos lo siguiente:
Ejemplo 2:
Si Ā = (6; 4), hallar el vector 2Ā y -2Ā.
Solución:
Veamos primero el vector 2Ā:
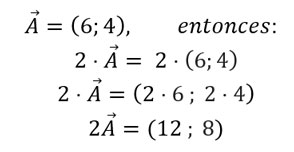
Veamos ahora el vector -2Ā:
Aunque el ejercicio no lo pide, vamos a graficar los vectores 2Ā y -2Ā:
Ejemplo 3:
Sabiendo que B̄ = (4; 6) y C̄ = (2; 1), calcular el valor del vector R si:
Solución:
Primero vamos a calcular el vector R̄, y luego calcularemos su módulo:
Ahora que ya tenemos el par ordenado que representa al vector R̄, podemos calcular su módulo teniendo en cuenta la siguiente fórmula:
En nuestro caso, R̄ = (8; 6), por lo tanto:
Ahora aplicamos la fórmula del módulo:
Guía de ejercicios
A continuación viene una guía con muchos ejercicios de vectores, resolveremos algunos en el video.
No hay comentarios.:
Publicar un comentario