El módulo de Young o módulo de elasticidad es la constante que relaciona el esfuerzo de tracción o compresión con el respectivo aumento o disminución de longitud que tiene el objeto sometido a estas fuerzas.
Las fuerzas externas aplicadas a los objetos no solamente pueden cambiar el estado de movimiento de estos, sino que también son capaces de cambiar su forma o incluso romperlos o fracturarlos.
El módulo de Young sirve para estudiar los cambios producidos en un material cuando se le aplica una fuerza de tracción o de compresión a nivel externo. Es muy útil en materias como la ingeniería o la arquitectura.
El modelo debe su nombre al científico británico Thomas Young (1773-1829), que fue quien llevo a cabo estudios de materiales proponiendo una medida de la rigidez de distintos materiales.
¿En qué consiste el modelo de Young?
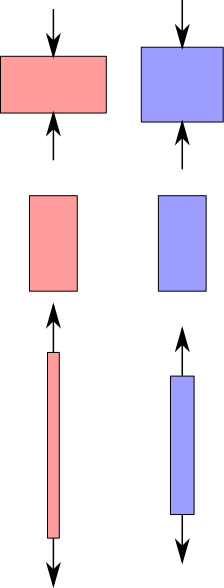
¿Cuánto se puede deformar un objeto? Esto es algo que los ingenieros con frecuencia quieren saber. La respuesta dependerá de las propiedades del material y de las dimensiones que tenga.
Por ejemplo, se pueden comparar dos barras hechas de aluminio con distintas dimensiones. Cada una tiene diferente área de sección transversal y longitud, y ambas son sometidas a una misma fuerza de tracción.
El comportamiento esperado será el siguiente:
– A mayor grosor (sección transversal) de la barra, menos estiramiento.
– A mayor longitud inicial, mayor estiramiento final.
Esto tiene sentido, porque al fin y al cabo, la experiencia señala que no es igual intentar deformar una liga de goma que intentar hacerlo con una varilla de acero.
Un parámetro llamado módulo de elasticidad del material es un indicativo de su respuesta elástica.
¿Cómo se calcula?
Siendo médico, Young quería conocer el papel de la elasticidad de las arterias en el buen desempeño de la circulación sanguínea. De sus experiencias concluyó la siguiente relación empírica:
El esfuerzo es proporcional a la deformación, mientras no se supere el límite elástico del material.
Es posible representar gráficamente el comportamiento de un material ante la aplicación de un esfuerzo, como se aprecia en la figura siguiente.
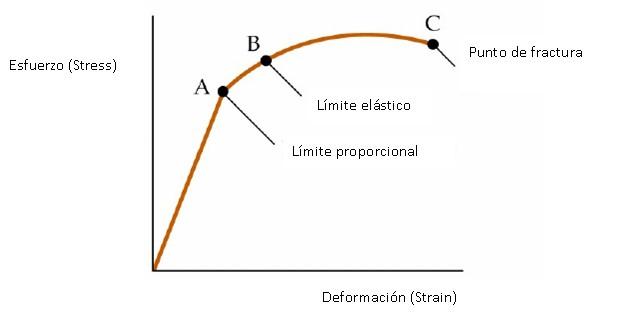
Del origen hasta el punto A
En el primer tramo, que va desde el origen hasta el punto A, la gráfica es una línea recta. Allí es válida la Ley de Hooke:
F = kx
Donde F es la magnitud de la fuerza que retorna al material a su estado original, x es la deformación experimentada por éste y k es una constante que depende del objeto sometido al esfuerzo.
Las deformaciones consideradas aquí son pequeñas y el comportamiento es perfectamente elástico.
Desde A hasta B
Desde A hasta B el material también se comporta de manera elástica, pero la relación entre esfuerzo y deformación ya no es lineal.
Desde B hasta C
Entre los puntos B y C, el material experimenta una deformación permanente, siendo incapaz de regresar a su estado original.
A partir de C
Si el material se sigue estirando a partir del punto C, finalmente sufre una ruptura.
Matemáticamente, las observaciones de Young pueden resumirse así:
Esfuerzo ∝ Deformación
Donde la constante de proporcionalidad es precisamente el módulo de elasticidad del material:
Esfuerzo = Módulo de elasticidad x Deformación
Existen muchas maneras de deformar los materiales. Los tres tipos de esfuerzo más comunes a los cuales someter un objeto son:
– Tensión o estiramiento.
– Compresión.
– Corte o cizalla.
Un esfuerzo al que comúnmente están sometidos los materiales, por ejemplo en la construcción civil o en las partes automotrices, es la tracción.
Fórmulas
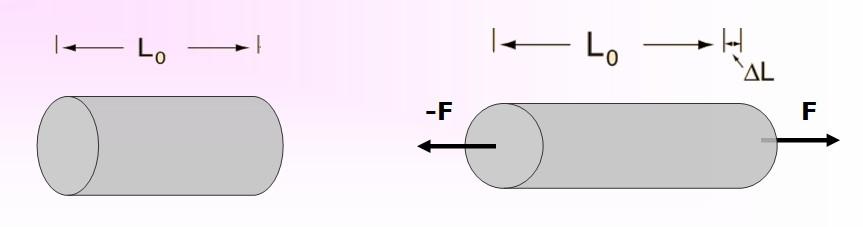
Cuando un objeto de longitud L se estira o se tensa, está siendo sometido a una tracción que ocasiona una variación en su longitud. Un esquema de esta situación se representa en la figura 3.
Ello requiere que se aplique una fuerza de magnitud F por unidad de área a sus extremos, para causar el estiramiento, de tal manera que su nueva longitud pasa a ser L + DL.
El esfuerzo realizado para deformar al objeto será justamente esta fuerza por unidad de área, mientras que la deformación unitaria experimentada es ΔL/L.
Denotando al módulo de Young como Y, y de acuerdo a lo dicho anteriormente:
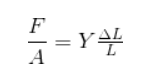¿Por qué se escoge específicamente la deformación unitaria y no simplemente la deformación a secas?
La respuesta está en el hecho de que la deformación unitaria indica la deformación relativa respecto a la longitud original. No es igual que una barra de 1 m se estire o se encoja 1 cm, a que una estructura de 100 metros de longitud se deforme igualmente 1 cm.
Para el buen funcionamiento de piezas y estructuras, hay una tolerancia en cuanto a las deformaciones relativas permitidas.
Ecuación para calcular la deformación
Si la ecuación anterior se analiza de la siguiente forma:
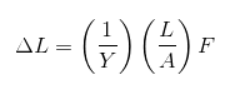Es fácil convencerse de que para una determinada fuerza F, cumple con las observaciones que hizo Young y que fueron descritas anteriormente:
– A mayor área de sección transversal, menor deformación.
– A mayor longitud, mayor deformación.
– A mayor módulo de Young, menor deformación.
Las unidades del esfuerzo corresponden a newton/metro cuadrado (N/m2). Son también las unidades de la presión, que en Sistema Internacional llevan el nombre de Pascal. La deformación unitaria ΔL/L en cambio, es adimensional por ser el cociente entre dos longitudes.
Las unidades del sistema inglés son lb/plg2 y también se emplean con mucha frecuencia. El factor de conversión para ir de una a otra es: 14.7 lb/plg2 = 1.01325 x 105 Pa
Esto lleva a que el módulo de Young tenga también unidades de presión. Finalmente, la ecuación anterior puede expresarse para despejar Y:
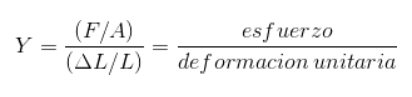Aplicaciones
En la ciencia de los materiales, la respuesta elástica de estos ante diversos esfuerzos es importante para seleccionar los más adecuados en cada aplicación, ya sea fabricar el ala de un avión o un rodamiento automotriz. Las características del material a emplear son decisivas en la respuesta que se espera de él.
Para escoger el mejor material, es necesario conocer los esfuerzos a los que va a estar sometida determinada pieza; y en consecuencia seleccionar el material que tenga las propiedades más acordes con el diseño.
Por ejemplo, el ala de un avión debe ser resistente, liviana y capaz de flexionarse. Los materiales empleados en la construcción de edificaciones han de resistir movimientos sísmicos en buena medida, pero también deben poseer cierta flexibilidad.
Los ingenieros que diseñan las alas de los aviones y también quienes escogen los materiales de construcción, deben hacer uso de gráficas de esfuerzo-deformación como la mostrada en la figura 2.
Es posible llevar a cabo las mediciones para determinar las propiedades elásticas más relevantes de un material en laboratorios especializados. Así, existen pruebas estandarizadas a las que se someten las muestras, a las que se aplican diversos esfuerzos, midiendo después las deformaciones resultantes.
Ejemplos
Como ya se mencionó anteriormente, Y no depende del tamaño o la forma del objeto, sino de las características del material.
Otro apunte muy importante: para que la ecuación dada anteriormente sea aplicable, el material debe ser isótropo, es decir, sus propiedades deben permanecer invariables en toda su extensión.
No todos los materiales son isótropos: los hay cuya respuesta elástica depende de ciertos parámetros direccionales.
La deformación analizada en los segmentos anteriores es apenas una de las muchas a las que se puede someter un material. Por ejemplo, en cuanto al esfuerzo de compresión, es el opuesto al esfuerzo de tensión.
Las ecuaciones dadas se aplican a ambos casos, y casi siempre los valores de Y son los mismos (materiales isótropos).
Una excepción notable es el concreto o cemento, el cual resiste mejor la compresión que la tracción. Por eso, debe reforzarse cuando se precisa resistencia al estiramiento. El acero es el material indicado para ello, pues resiste muy bien los estiramientos o tracciones.
Como ejemplos de estructuras sometidas a esfuerzos están las columnas de las edificaciones y los arcos, elementos clásicos de construcción en muchas civilizaciones antiguas y modernas.
Ejercicios resueltos
Ejercicio 1
Un alambre de acero de 2.0 m de largo en un instrumento musical tiene un radio de 0.03 mm. Cuando el cable está bajo una tensión de 90 N: ¿cuánto cambia su longitud?Dato: el módulo de Young del acero es 200 x 109 N/m2
Solución
Se requiere calcular el área de la sección transversal A = πR2 = π. (0.03 x 10-3 m)2 =2.83 x 10-9 m2
El esfuerzo es la tensión por unidad de área:
Por lo tanto ΔL = 0.16 x 2 m = 0.32 m
Como la cuerda se encuentra bajo tensión, esto significa que se alarga.
La nueva longitud es L = Lo + DL, donde Lo es la longitud inicial:
L=2.32 m
Ejercicio 2
Una columna de mármol, cuya área de sección transversal es de 2.0 m2 sostiene una masa de 25.000 kg. Encontrar:
a) El esfuerzo en la columna.
b) La deformación unitaria.
c) ¿En cuánto se acorta la columna si su altura es de 12 m?
Dato: el módulo de Young del mármol es 50 x 109 N/m2
Solución
a) El esfuerzo en la columna es debido al peso de los 25000 kg:
P = mg = 25000 kg x 9.8 m/s2 = 245.000 N
Por lo tanto el esfuerzo es:
b) La deformación unitaria es ΔL/L:
c) ΔL es la variación de la longitud, dada por:
ΔL = 2.45 x 10-6 x 12 m =2.94 x10-5 m = 0.0294 mm.
No se espera que la columna de mármol se encoja significativamente. Obsérvese que si bien el módulo de Young es menor en el mármol que en el acero, y que además la columna soporta una fuerza mucho mayor, su longitud casi no varía.
En cambio, en la cuerda del ejemplo anterior la variación bastante más apreciable, aunque el acero tiene un módulo de Young mucho mayor.
En la columna interviene su gran área de sección transversal, y por eso es mucho menos deformable.
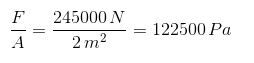
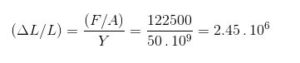
No hay comentarios.:
Publicar un comentario