Leyes de los signos para multiplicación y división

Regla de los signos

La regla de los signos nos permite saber el signo que debe tener el resultado del producto de dos números.
La regla es la misma para la división.

Vamos a escribir esta regla en forma de cuatro reglas:

$+\cdot +=+$

$-\cdot -=+$

$+\cdot -=-$

$-\cdot +=-$

• La primera regla es "$+\cdot +=+$", lo que significa que al multiplicar dos números positivos se obtiene un número positivo:
  

  $(+3)\cdot (+4)=+12$

• La segunda regla es "$-\cdot -=+$", lo que significa que al multiplicar dos números negativos se obtiene un número positivo:
  

  $(-3)\cdot (-4)=+12$

• La tercera regla es "$+\cdot -=-$", lo que significa que al multiplicar un número positivo por uno negativo se obtiene un número negativo:
  

  $(+3)\cdot (-4)=-12$

• La cuarta regla es "$-\cdot +=-$", lo que significa que al multiplicar un número negativo por uno positivo se obtiene un número negativo:
  

  $(-3)\cdot (+4)=-12$

Es decir, si los dos números tienen el mismo signo (los dos negativos o los dos positivos), entonces su producto es un número positivo. Y si tienen signo distinto, su producto es un número negativo.
Casos especiales y comentarios:

• Si alguno de los dos números es 0, entonces el resultado es 0 (ni positivo ni negativo):
  

  $(-3)\cdot 0=0$

  $0\cdot (+4)=0$

• Los números que son positivos pueden escribirse sin signo y sin paréntesis:
  

  $(-3)\cdot 3=-9$

  $5\cdot 2=10$

• Los números que son negativos y están a la izquierda pueden escribirse sin paréntesis:
  

  $-3\cdot 2=-6$

  $-5\cdot (-6)=30$

• La regla es la misma para la división:
  

  $15:3=5$

  $(-3):(-3)=1$

  $(-6):2=-3$

  $4:(-2)=-2$

• ______________________________________________

Producto

Si el número del multiplicando es mayor que dos se pondrá a la respuesta signo negativo solo si la cantidad total de signos negativos es impar, si la cantidad de negativos es par o cero se pondrá signo positivo

Ejemplos

                        (8)(2)(3) = 48

                        (-1)(-5)(3)(-2) = -30

                        (x)(z)(-y) = - xyz

                        (12x)(-3y)(8z) = -288xyz
-------------------------------------------------

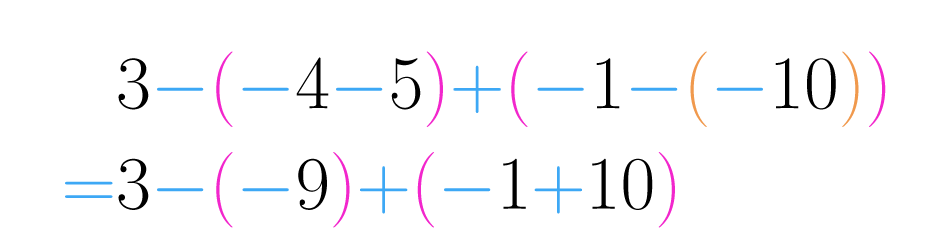
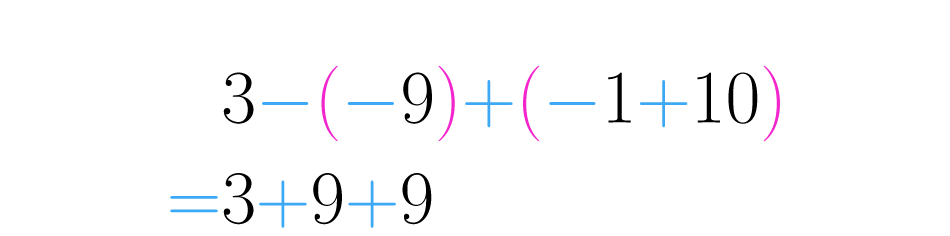
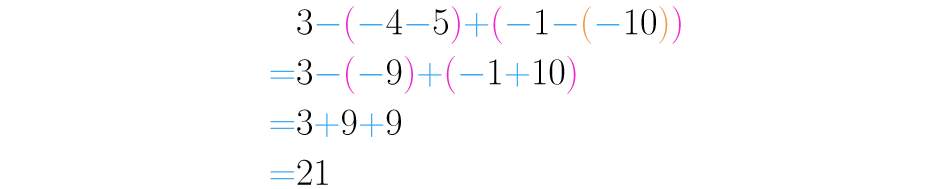
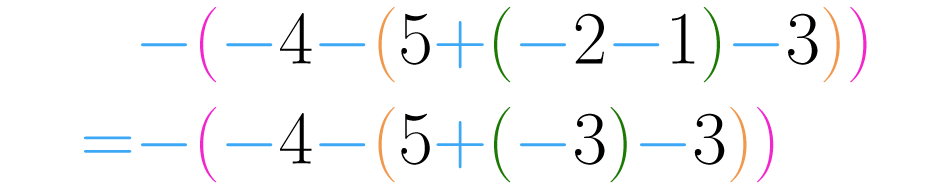
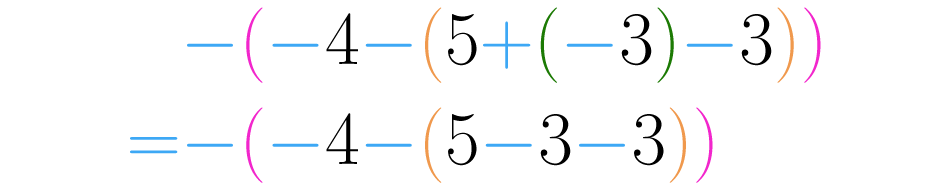
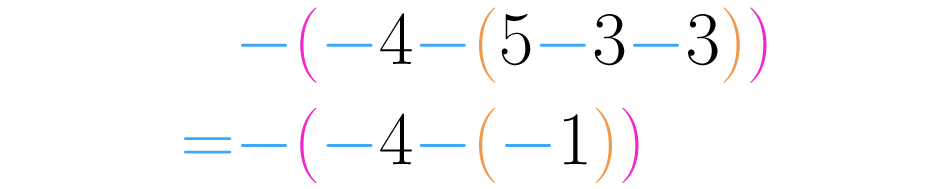
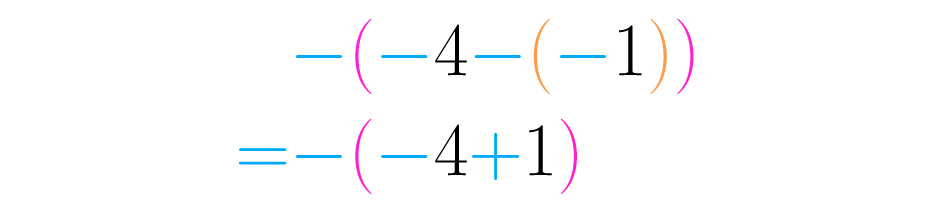
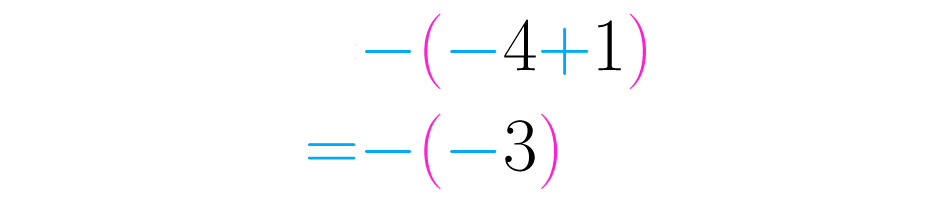
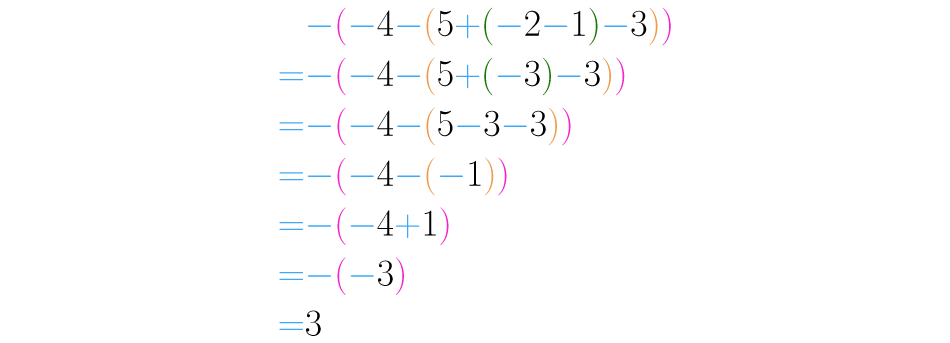
Ley de los signos para multiplicación y división

Para estas operaciones también existen diversas normas muy parecidas a la suma

• En el caso de multiplicar o dividir un signo positivo con otros positivo el resultado es positivo.
• De multiplicar o dividir un signo negativo con otro negativo el resultado será positivo.
• Por último si se multiplica o divide un signo negativo con uno positivo o viceversa siempre será negativos, sin tomar en cuenta el mayor valor del número.

(+6) ÷ (+4)= +1,5
(-8) ÷ (-4)= +2
(+4) ÷ (-2)= -2

________________________________________

Simplificación de expresiones con ley de signos

Estudiaremos ahora la forma correcta de resolver expresiones del tipo  Observa una forma de hacerlo:

Paso 1:

Debemos resolver primero los paréntesis más pequeños.  La resta  da como resultado  y según la ley de signos .

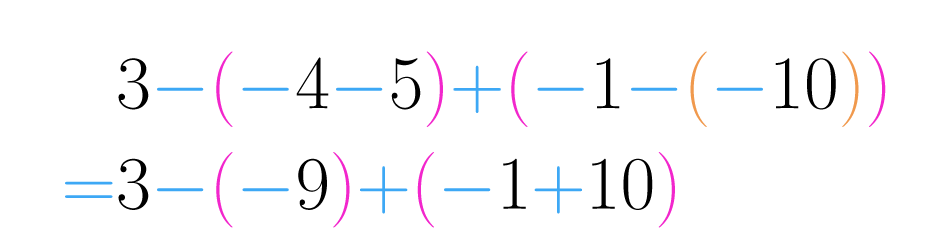
Paso 2:

Siguiendo con la simplificación de los paréntesis que quedan:   y .  Así, llegamos a la expresión .

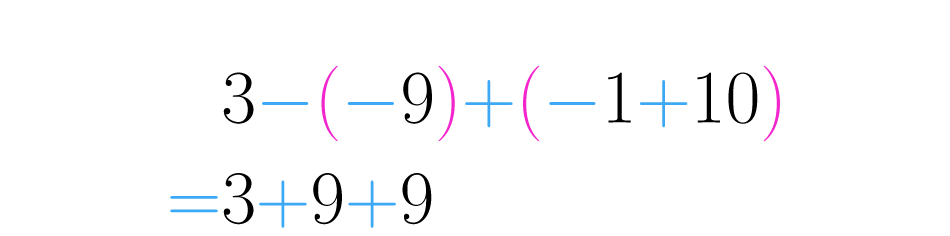
Paso 3:

Una vez que se han simplificado todos los signos consecutivos, es fácil continuar.  Realizamos la suma .  Observa el procedimiento completo:

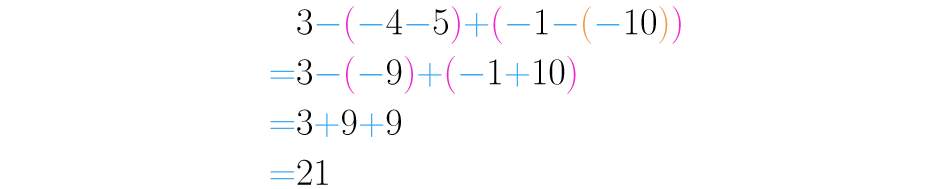
Observa que solo usamos la ley de signos cuando encontramos los símbolos  y  consecutivos.  Esta ley nunca se debe usar para resolver las sumas o las retas.  Estaría mal usarla para resolver .

Otro ejemplo

Simplifiquemos la expresión :

En esta ocasión tenemos varios paréntesis anidados, es decir, que están uno dentro del otro.  Los resolvemos paso a paso desde los más pequeños hasta los más grandes.

Paso 1:

Comenzamos resolviendo los paréntesis más pequeños.  Operamos , que da como resultado .

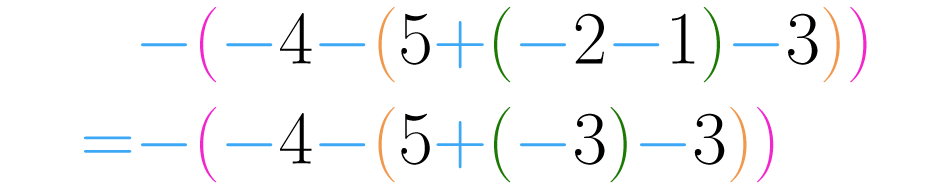
Paso 2:

Ahora el paréntesis más pequeño es , pero este está precedido por un signo .  Debemos entonces usar la la ley de signos: “más por menos, menos”, obtenemos así: :

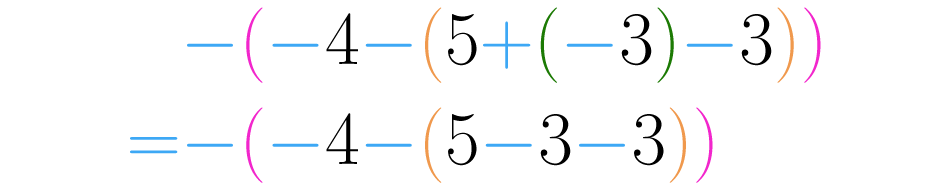
Paso 3:

A medida que avancemos, debemos realizar las operaciones que vayan apareciendo, en este caso:  .

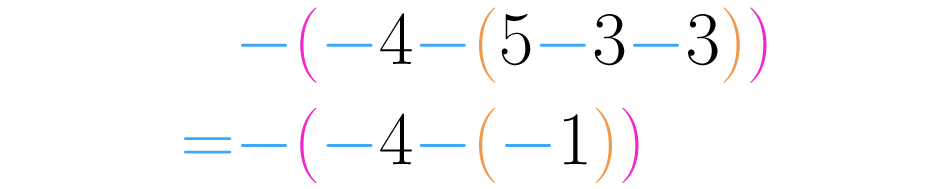
Paso 4:

De nuevo, usando la ley de signos, , así resolvemos un paréntesis más:

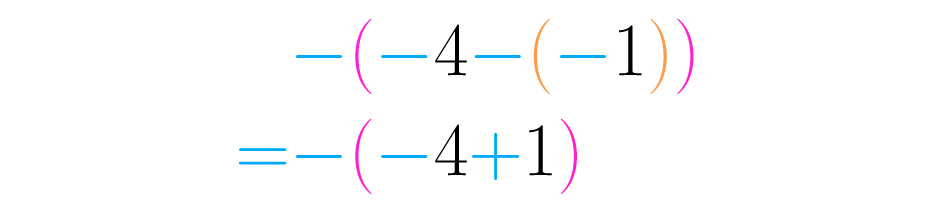
Paso 5:

Recuerda realizar las sumas y las restas sin signos consecutivos a medida que van apareciendo: :

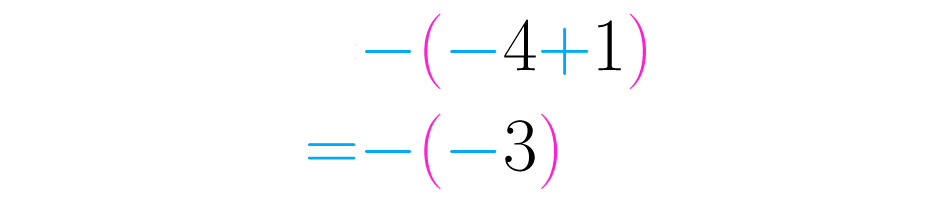
Paso 6:

Finalmente, aplicamos la ley de los signos a : “menos por menos, más”.  Llegamos así a la respuesta final: .  En la siguiente imagen puedes ver el proceso completo:

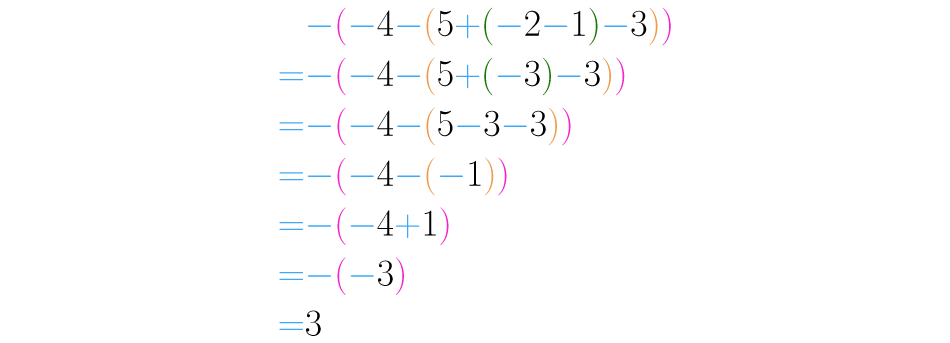
Como te puedes dar cuenta, aplicamos la ley de signos al encontrar signos  y  consecutivosy operamos los números enteros según aparezcan sumando o restando como ya sabemos.