Jerarquia de las operaciones matemáticas

Jerarquía de operaciones. Como resolver operaciones combinadas.

A continuación voy a explicarte qué es la jerarquía de operaciones para poder realizar operaciones combinadas con sumas, restas, multiplicaciones, paréntesis y potencias a la vez.

Vemos también cómo resolver operaciones combinadas con paréntesis y corchetes, además de explicarte cómo resolver operaciones combinadas con potencias  y raíces.

Operaciones combinadas y la jerarquía de operaciones

Cuando hablamos de jerarquía de operacioneshablamos del orden en el que se deben realizar las operaciones en las expresiones matemáticas donde tenemos más de una operación, sumas, restas, multiplicaciones, divisiones, potencias…, es decir, en operaciones combinadas

Dicho de otra forma, es la prioridad que tienen unas operaciones frente a otras a la hora de resolverlas, teniendo en cuenta su nivel dentro de la jerarquía

Cómo se resuelven las operaciones combinadas

Cuando tenemos expresiones donde se combinan operaciones, debemos empezar resolviendo las operaciones por el primer nivel, teniendo en cuenta las siguiente premisas:

• No podemos mezclar operaciones de distinto nivel
• El objetivo es reducir los niveles hasta llegar al más simple, que es donde sólo hay sumas y restas
• Los paréntesis deben resolverse como si se trataran de expresiones individuales, por lo que debe aplicarse la jerarquía de operacionesindependientemente del resto de la expresión.

Jerarquía de operaciones. Prioridad de operaciones matemáticas

Éste es el orden en el que deben realizarse las diferentes operaciones que pueden existir en una expresión matemática:

1. Paréntesis, corchetes o llaves (se resuelven de dentro hacia afuera)
2. Potencias y raíces
3. Multiplicaciones y divisiones
4. Sumas y restas

Jerarquía de operaciones combinadas con sumas y restas

Estas operaciones aunque no tienen mayor complicación, ya que todas las operaciones están al mismo nivel de la jerarquía. Solamente hay que operar y ya está:

El objetivo es reducir las expresiones con operaciones en varios niveles hasta este nivel.

Jerarquía de operaciones combinadas con sumas, restas, multiplicaciones y divisiones

Vamos a incorporar multiplicaciones y divisiones:

Ahora hay que realizar primero multiplicaciones y divisiones, que están en un nivel superior en la jerarquía:

Y nos vuelve a queda solamente sumas y restas, como en el caso anterior:

Jerarquía de operaciones combinadas con sumas, restas, multiplicaciones, divisiones y potencias

Incorporamos en este caso una potencia:

En este caso, debemos resolver la potencia primero para poder multiplicarlo por 13:

Una vez eliminadas las potencias, nos encontramos en el caso anterior, así que se resuelve de la misma manera:

En este caso primero hemos resuelto la potencia, luego las multiplicaciones y divisiones y después sumas y restas. Vamos eliminando niveles.

Jerarquía de operaciones combinadas con sumas, restas, multiplicaciones, divisiones, potencias y paréntesis

Ahora vamos a ver el caso de que tengamos un paréntesis y dentro del paréntesis tengamos potencias, multiplicaciones y divisiones y sumas y restas:

Tenemos que resolver el paréntesis como si fuera una expresión a parte, o con otras palabras, aplicar la jerarquía de operaciones dentro del paréntesis y olvidarnos del resto:

Hemos resuelto las potencias. El siguiente paso es resolver las multiplicaciones y divisiones dentro del paréntesis:

Ahora solo queda sumar dentro del paréntesis:

Volvemos a tener multiplicaciones, sumas y restas, por lo que estamos como en el segundo apartado:

Jerarquía de operaciones combinadas con sumas, restas, multiplicaciones, divisiones, potencias y paréntesis con potencias

En este caso vamos a añadir otro paréntesis con una potencia:

Resolvemos primero el paréntesis con la potencia:

Y ahora resolvemos la potencia que nos queda:

Ahora estamos en el mismo punto que en el apartado anterior, por lo que resolvemos igual:

Operaciones combinadas con potencias y raíces

Las potencias y raíces se encuentran en el segundo nivel de la jerarquía de operaciones, por encima de las multiplicaciones y divisiones y por tanto deben resolverse antes que éstas.

No tienes que aprenderte en qué nivel está cada una de las operaciones, ya que el sentido común te dirá qué hacer, tal y como vamos a ver en este ejemplo:

En esta operación tenemos sumas, restas, multiplicaciones y potencias.

Vamos olvidarnos por un momento de la potencia. Sabemos, por la lección anterior, que antes de las sumas y restas hay que resolver multiplicaciones y divisiones.

Pero en este caso, no podemos realizar la multiplicación si antes no resolvemos la potencia. Es por eso, que las potencias y las raíces están un nivel por encima de las multiplicaciones y divisiones. ¿Ves por qué digo que es de sentido común?

Resolvemos por tanto, primero las potencias:

Nos ha quedado una operación con multiplicaciones, sumas y restas, por lo que resolvemos la multiplicación:

Y finalmente realizamos las sumas y restas:

Con las raíces ocurre exactamente lo mismo. Vamos a verlo con otro ejemplo:

Tenemos una raíz dentro de una división, que no se puede realizar hasta que no se resuelva la raíz. Por tanto lo primero que hay que hacer es resolver la raíz:

Ahora ya se puede realizar la división:

Y finalmente las sumas y restas:

Cómo resolver paréntesis

Vamos a ver ahora cómo eliminar los paréntesis en las operaciones. Esta vez me refiero a los paréntesis que encierran más de un término, ya que, como ya sabes, también existen los paréntesis que encierran los números negativos, que se ponen para no tener dos signos seguidos.

Vamos a empezar con un ejemplo muy sencillo:

En este caso tenemos un paréntesis con 2 términos. Para eliminarlo, debemos operar dentro del paréntesis como si se tratara de una operación aislada. Realizamos la resta:

Nos ha quedado un paréntesis con un término. Por tanto, lo eliminamos siguiendo la regla de los signos y ya podemos terminar la operación:

Cuando se opera dentro del paréntesis, también hay que tener en cuenta la jerarquía de operaciones. Vamos a verlo con este otro ejemplo:

En primer lugar, tenemos que resolver el interior del paréntesis, pero en este caso, tenemos una multiplicación, que tendremos que resolver la primera:

Seguimos con las sumas y restas dentro del paréntesis:

Y para terminar, eliminamos el paréntesis según el signo que tenga delante y terminamos la operación:

Vamos a ver ahora este otro ejemplo, donde tenemos dos paréntesis:

Dentro de uno de ellos, tenemos una multiplicación, que pasamos a resolver, dejando el resto de la operación tal y como está:

Ahora, realizamos las sumas y restas de cada uno de los paréntesis:

Eliminamos el paréntesis según el signo que lleven delante y terminamos la operación:

Seguimos con otro ejemplo, en el que el paréntesis está multiplicado por un número, es decir, forma parte de una multiplicación:

El primer paso como siempre sería resolver el paréntesis:

Y una vez resuelto, realizamos la multiplicación y posteriormente las sumas que nos queda:

De la misma forma, el paréntesis puede formar parte de una división:

Resolvemos primero el paréntesis:

Y seguimos con la división y para terminar con la resta:

También podemos tener dos paréntesis multiplicándose entre sí:

En este caso, al resolver cada paréntesis por separado, se nos queda una simple multiplicación:

¿Vas captando el procedimiento? Al resolver los paréntesis en primer lugar, la operación se va simplificando y nos quedan expresiones en las que el siguiente paso es resolver primero multiplicaciones y divisiones y por último, sumas y restas.

Operaciones combinadas con paréntesis y corchetes

Vamos a aumentar un grado más la dificultad y vamos a ver ahora cuando tenemos paréntesis dentro de otros paréntesis o mejor dicho, paréntesis dentro de corchetes, ya que los paréntesis que encierran a otros paréntesis se llaman corchetes [].

En primer lugar, podemos tener corchetes cuando tenemos ya un número negativo encerrado entre paréntesis, como en esta operación:

Si te das cuenta, en este caso, resolver el corchete es igual que resolver los paréntesis que hemos estado resolviendo hasta ahora. Resolvemos la suma:

Y ahora eliminamos el paréntesis teniendo en cuenta el signo que tiene delante y terminamos la operación:

Es algo más complicado, resolver corchetes, que dentro tengan paréntesis con más de un término. En estos casos, tenemos que empezar por resolver los paréntesis de dentro y los corchetes se convertirán en simples paréntesis.

Vamos a verlo con el siguiente ejemplo:

En esta operación se necesitan los corchetes porque dentro tenemos paréntesis con más de un término que hay que resolver. Por tanto, el primer paso es resolver los paréntesis de dentro del corchete:

Ahora eliminamos los paréntesis (que simplemente se quitan porque son números positivos) y los corchetes se convierten en paréntesis, al no tener paréntesis dentro.

Nos queda ahora una operación con un paréntesis, que tenemos que resolver, empezando por la división que tiene dentro:

Resolvemos el paréntesis:

Y finalmente, eliminamos el paréntesis y realizamos la resta:

Vamos a ver otro ejemplo de cómo resolver operaciones combinadas con paréntesis y corchetes:

Esta operación tiene más de un camino para resolverse. Puedes probar a hacerla por tu cuenta y comprobar después si tu resultado es el mismo

Yo voy a empezar resolviendo el paréntesis que está dentro de los corchetes:

Al resolver el paréntesis (que da un número positivo) los corchetes se han convertido en paréntesis.

Ahora voy a realizar la multiplicación del segundo paréntesis:

Resolvemos los paréntesis:

Por último eliminamos paréntesis y realizamos las sumas resultantes:

Un último ejemplo para terminar:

Resolvemos los paréntesis que hay dentro de los corchetes:

Resolvemos el paréntesis con dos términos y realizamos la división:

Ejercicios propuestos de operaciones combinadas con paréntesis y potencias

Resuelve las siguientes operaciones:

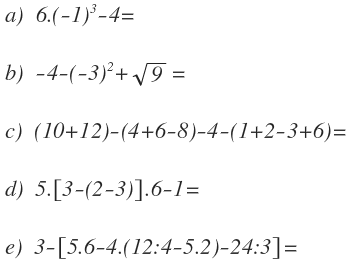
Ejercicios resueltos de operaciones combinadas con fracciones

Vamos a explicarlo con unos cuantos ejemplos resueltos de operaciones combinadas con fracciones. Nos detendremos en qué es lo que necesitas saber en cada uno de los pasos.

Ejemplo 1:

Tenemos dos operaciones: suma y multiplicación. Pues en primer lugar realizamos la multiplicación:

Nos ha quedado una suma con distinto denominador. Ahora obtenemos común denominador y realizamos la suma:

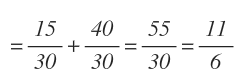
Al final, hemos simplificado la fracción.

Ejemplo 2:

En este caso tenemos varias operaciones combinadas con fracciones y además paréntesis y corchetes.

¿Por donde empezar? Pues hay que empezar eliminando paréntesis y la única forma de hacerlo es empezando por el que más adentro está. Recuerda que cuando tenemos varios paréntesis hay que empezar de dentro hacia afuera:

Ya hemos eliminado el paréntesis de dentro y nos ha quedado un sólo paréntesis. Procedemos a resolverlo:

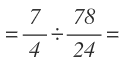
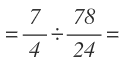
Por último, nos queda una división, que la resolvemos multiplicando en cruz:

Ejemplo 3

Vamos a aumentar un poco más la dificultad. Pero tranquilo. Ya verás como si vas resolviendo paso por paso, cada se va volviendo un poco más fácil:

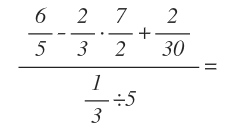
Esta vez, podemos realizar más de una operación en el mismo paso, ya que no dependen una de la otra. Por tanto empezamos haciendo la multiplicación del numerador y la división del denominador:

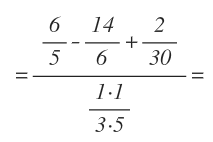
Ahora en el numerador nos han quedado 3 fracciones para sumar y restar con distinto denominador. Las transformamos a común denominador. Para ello recordamos que necesitamos obtener el mínimo común múltiplode los denominadores, para luego obtener sus fracciones equivalentes:

Una vez realizadas todas las operaciones en el numerador y en el denominador, solamente queda realizar la división entre las fracciones finales y simplificar el resultado: