1. Introducción
Cuando el integrando está formado por un producto (o una división, que podemos tratar como un producto) se recomienda utilizar el método de integración por partes que consiste en aplicar la siguiente fórmula:
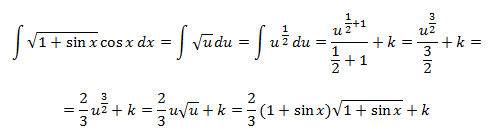
Método:
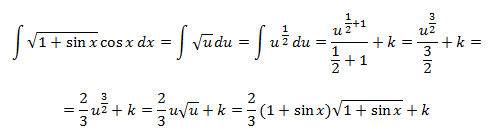
Método:
- El integrando debe ser un producto de dos factores.
- Uno de los factores será u y el otro será dv.
- Se calcula du derivando u y se calcula vintegrando dv.
- Se aplica la fórmula.
2. Consejos
- Escoger adecuadamente u y dv:
Una mala elección puede complicar más el integrando.
Supongamos que tenemos un producto en el que uno de sus factores es un monomio (por ejemplo x3). Si consideramos dv = x3. Entonces, integrando tendremos que v = x4/4,con lo que hemos aumentado el grado del exponente y esto suele suponer un paso atrás.
Normalmente, se escogen los monomios como u para reducir su exponente al derivarlos. Cuando el exponente es 0, el monomio es igual a 1 y el integrando es más fácil.
Algo parecido ocurre con las fracciones (como 1/x). Si consideramos dv = 1/x, tendremos v = log|x| y, probablemente, obtendremos una integral más difícil.
Como norma general, llamaremos ua las potencias y logaritmos y dv a las exponenciales, fracciones y funciones trigonométricas. - No cambiar la elección:
A veces tenemos que aplicar el método más de una vez para calcular una misma integral.
En estas integrales, al aplicar el método por n-ésima vez, tenemos que llamar u al resultado du del paso anterior y dv al resultado v. Si nolo hacemos así, como escoger una opción u otra supone integrar o derivar, estaremos deshaciendo el paso anterior y no avanzaremos. - Integrales cíclicas:
En ocasiones, tras aplicar dos veces integración por partes, tenemos que despejar la propia integral de la igualdad obtenida para poder calcularla. Un ejemplo de esto es la Integral 10.
3. 21 Integrales resueltas
Integral 1
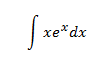
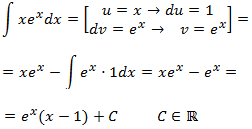
Nota: es importante escoger
ya que de este modo estamos reduciendo el grado del monomio (de 1 a 0). Si por el contrario escogemos
aumentamos el grado (de 1 a 2) y complicamos más la integral ya que el factor de la exponencial se mantiene igual y nos queda la integral
Integral 2
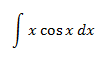
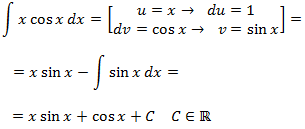
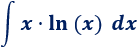
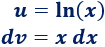
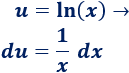
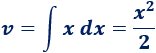
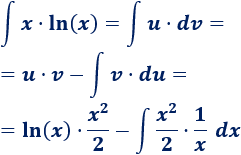
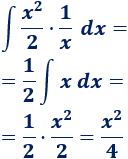
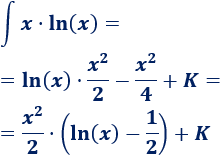
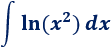
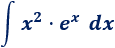
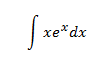
Solución
Integramos por partes:
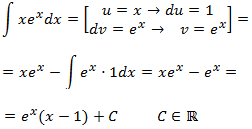
Nota: es importante escoger
Integral 2
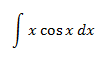
Solución
Integramos por partes:
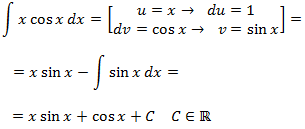
Nota: al igual que en el ejercicio anterior, como no importa si cos x es u ó dv (ya que obtenemos un sinus), elegimos u = x para disminuir su grado (y así desaparece la x). Si escogemos dv = x, aumentamos su grado:
Integración por partes
En esta página explicamos el método de integración por partes paso a paso. Calcularemos 11 integrales mediante este método para ver el procedimiento. Este método se basa en la aplicación de la siguiente fórmula:
donde
- es una función y es su derivada
- es una función y es su derivada
El método se aplica, sobre todo, cuando el integrando es un producto de funciones.
Notación: escribiremos la función logaritmo natural (logaritmo en base como .
Ejemplo
Calculamos la integral
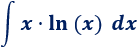
El integrando es un producto de dos funciones.
1. Identificamos y
Es importante pensar la elección de y porque luego tenemos que derivar e integrar . Además, tenemos que calcular la integral de la fórmula.
Si escogemos , entonces su derivada es . Pero, entonces, tenemos que escoger y para calcular tenemos que integrar el logaritmo.
Por tanto, escogemos la otra opción:
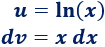
2. Calculamos y
Para calcular tenemos que derivar :
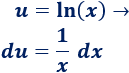
Para calcular tenemos que integrar :
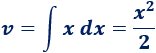
3. Aplicamos la fórmula
Sólo tenemos que sustituir las variables de la fórmula:
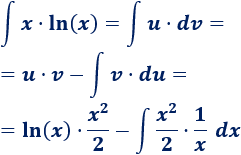
4. Calculamos la integral que queda
La integral que queda es inmediata:
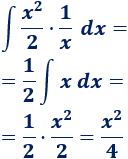
Por tanto,
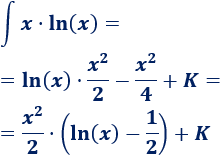
No olvidéis la constante de integración .
------------------------------------------------
Integral 1
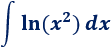
Solución
Antes que nada, aprovechamos las propiedades de los logaritmos para simplificar el integrando:
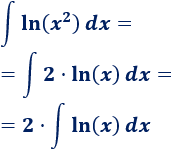 Vamos a calcular la integral del logaritmo natural (luego ya multilicaremos por 2).
Vamos a calcular la integral del logaritmo natural (luego ya multilicaremos por 2).
Podemos escribir el integrando como un producto para ver claramente la aplicación de la fórmula:
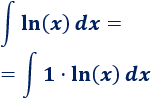
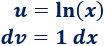
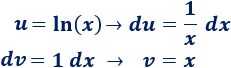
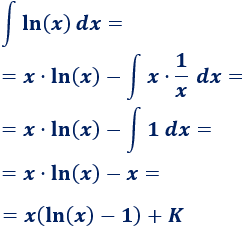 Por tanto, la integral del problema es
Por tanto, la integral del problema es
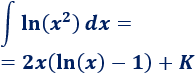
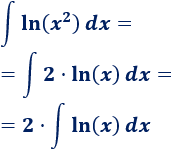
Podemos escribir el integrando como un producto para ver claramente la aplicación de la fórmula:
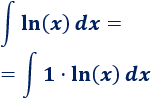
1. Identificamos y
Obviamente, no debemos escoger ya que entonces, tendríamos que calcular la integral del logaritmo, que es precisamente lo que estamos haciendo. Por tanto,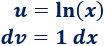
2. Calculamos y
Derivamos e integramos: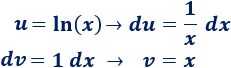
3. Aplicamos la fórmula
Sustituimos en la fórmula: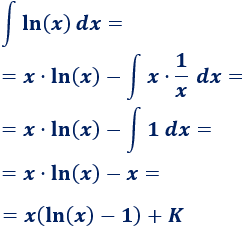
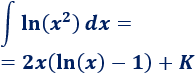
------------------------------------------------
Integral 2
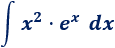
Solución
El integrando es un producto de dos funciones.
Si escogemos , tendremos que calcular la integral
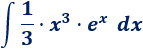 Así que es mejor escoger para bajar el grado del monomio.
Así que es mejor escoger para bajar el grado del monomio.
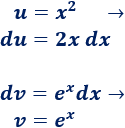
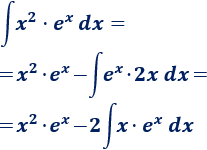 Aplicamos de nuevo integración por partes para calcular la integral que nos queda. Para no deshacer los cálculos anteriores, mantenemos la elección de y :
Aplicamos de nuevo integración por partes para calcular la integral que nos queda. Para no deshacer los cálculos anteriores, mantenemos la elección de y :
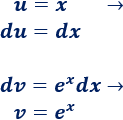 Por tanto,
Por tanto,
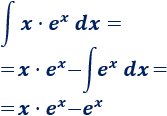 Volviendo al comienzo,
Volviendo al comienzo,
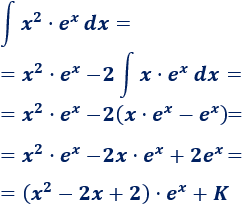

Escogemos para rebajar su grado.
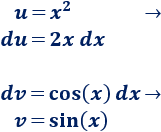
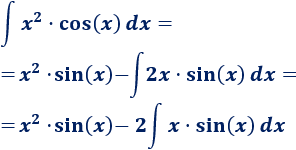 Aplicamos de nuevo integración por partes para calcular la integral que nos falta. Como dijimos en el problema anterior, debemos mantener la elección de los factores y :
Aplicamos de nuevo integración por partes para calcular la integral que nos falta. Como dijimos en el problema anterior, debemos mantener la elección de los factores y :
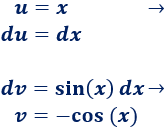 Aplicamos la fórmula:
Aplicamos la fórmula:
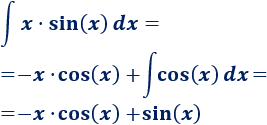 Por tanto,
Por tanto,
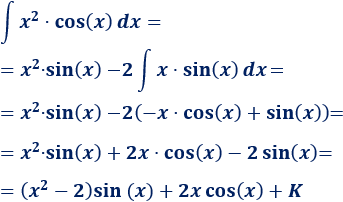
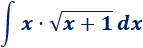
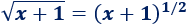 La derivada de es inmediata:
La derivada de es inmediata:
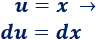 Calculamos integrando :
Calculamos integrando :
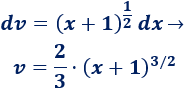 Por si lo necesitáis, vamos a escribir el cálculo de :
Por si lo necesitáis, vamos a escribir el cálculo de :
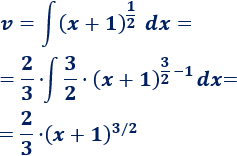
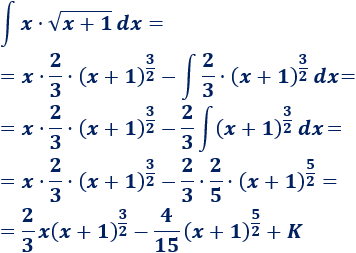 Si operamos un poco, el resultado final queda como
Si operamos un poco, el resultado final queda como
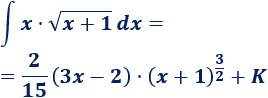
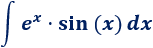
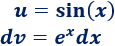
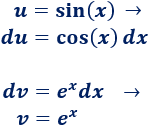
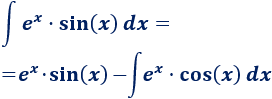 Aplicamos de nuevo integración por partes:
Aplicamos de nuevo integración por partes:
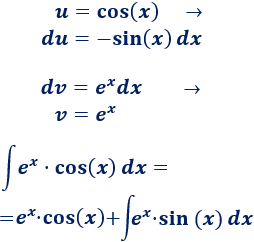 Volviendo al comienzo, tenemos
Volviendo al comienzo, tenemos
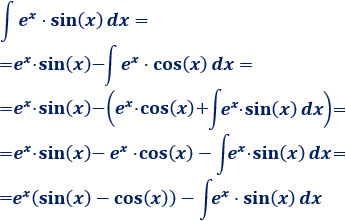 Pasamos la integral del lado derecho sumando al lado izquierdo:
Pasamos la integral del lado derecho sumando al lado izquierdo:
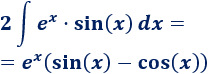 De donde podemos aislar la integral que buscamos:
De donde podemos aislar la integral que buscamos:
1. Identificamos y
No importa si es ó porque tanto su derivada como su integral es .Si escogemos , tendremos que calcular la integral
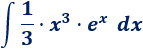
2. Calculamos y
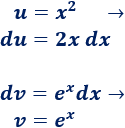
3. Aplicamos la fórmula
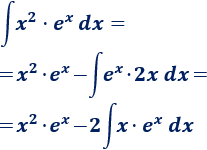
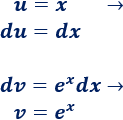
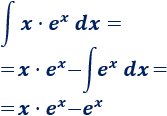
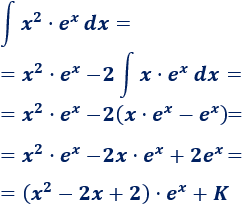
Integral 3

Solución
1. Identificamos y
No importa si es ó porque tanto su integral como su derivada son .Escogemos para rebajar su grado.
2. Calculamos y
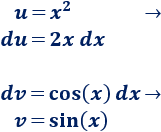
3. Aplicamos la fórmula
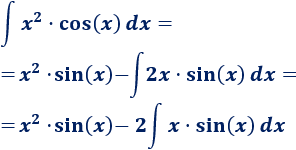
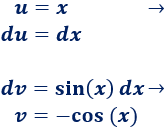
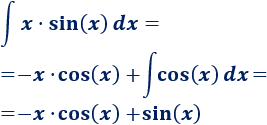
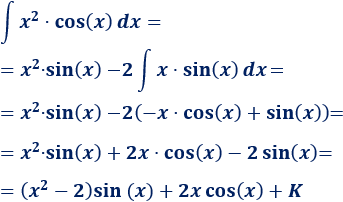
Integral 4
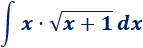
Solución
1. Identificamos y
Como en los problemas anteriores, escogemos para rebajar su grado.2. Calculamos y
Vamos a escribir la raíz como una potencia: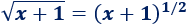
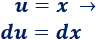
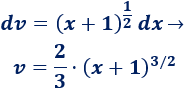
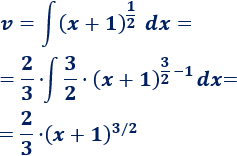
3. Aplicamos la fórmula
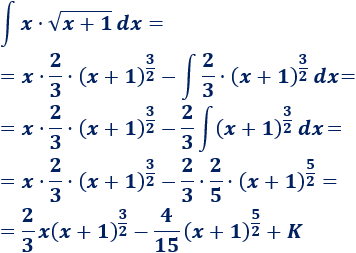
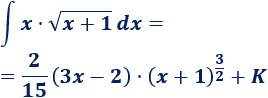
Integral 5
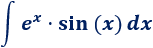
Solución
1. Identificamos y
En esta integral no importa cuáles sean y porque es irrelevante derivar o integrar la exponencial o el seno. Escogemos, por ejemplo,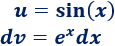
2. Calculamos y
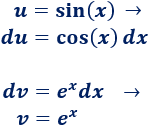
3. Aplicamos la fórmula
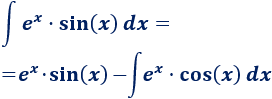
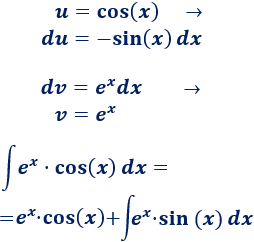
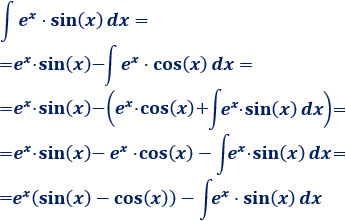
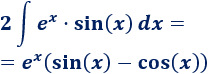
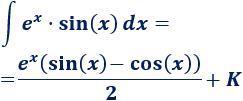
No hay comentarios.:
Publicar un comentario