Propiedades de la integral definida. Ejercicios resueltos paso a paso

Vamos a ver las propiedades de la integral definida, las cuales vamos a necesitar aplicar para resolver ejercicios de cálculo de áreas. Aplicaremos las propiedades resolviendo algunos ejercicios paso a paso.

Si has llegado hasta aquí es porque necesitas un profesor de matemáticas online. Si después de leer esto, quieres que te ayude a entenderlas de verdad, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.

Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:

Índice de Contenidos [Ocultar]

Propiedades de la integral definida

Las propiedades de la integral definida son las siguientes:

Integral definida entre dos limites de integración iguales

La integral definida entre dos límites de integración iguales, es decir, cuando el límite superior de integración y el límite inferior son iguales, entonces su resultado es igual a cero:

Esto es así, porque realmente no estamos calculando el área entre dos límites de integración

Integral definida de una función positiva

Si una función es positiva dentro de un intervalo [a,b], es decir, que en ese intervalo la función queda por encima del eje x, la integral definida es positiva, cuyos límites de integración son los límites de ese intervalo:

Por tanto, el área limitada por la función, en eje x y los valores a y b, es igual a la integral definida en ese intervalo:

Integral definida de una función negativa

Siguiendo la misma línea que la propiedad anterior, si una función es negativa dentro de un intervalo [a,b], es decir, que en ese intervalo la función queda por encima del eje x, la integral definida es negativa, cuyos límites de integración son los límites de ese intervalo:

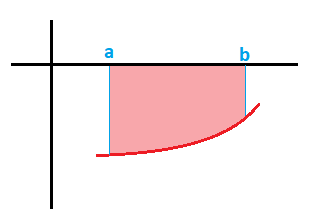
En este caso, el área limitada por la función, en eje x y los valores a y b, es igual a la integral definidaen ese intervalo, precedida por un signo menos:

Esto es así, ya que los valores de un área siempre son positivos. Como en este caso, el valor de la integral será negativo, debemos volverla positivo con un signo menos delante.

Esta propiedad se debe utilizar cuando el área que te pidan calcular, se quede por debajo del eje x.

Si la función cambia de signo en un determinado intervalo, el área de ese intervalo será la suma de las áreas de cada recinto.

Por ejemplo, tenemos una función cambia de signo en un intervalo [a,d]:

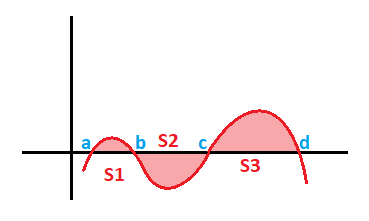
En este caso nos quedan 3 recintos: uno definido entre los puntos a y b, que llamaremos S1, otro definido entre los puntos b y c, que llamaremos S2 y otro entre los puntos c y d que llamaremos S3. El área limitada por la función, el eje x y los puntos a y d será la suma de esos tres recintos:

O lo que es lo mismo, la suma de las respectivas integrales definidas, afectadas por su signo correspondiente, en función de si quedan por encima o por debajo del eje x:

Vemos que la integral definida entre b y c es negativa por quedar por debajo del eje x.

Integral definida entre puntos del interior del intervalo

Si tenemos un punto c, que pertenece al intervalo [a,b], el área limitada en ese intervalo es igual al área limitada entre los puntos de abcisa a y c, más el área limitada entre los puntos de abcisa b y c y por tanto, lo mismo ocurre con el valor de la integral definida:

Esta propiedad se puede generalizar a tomar más puntos dentro del intervalo [a,b].

Date cuenta que con esta propiedad también se cumple lo mismo que en la propiedad anterior, para las funciones que cambian de signo: el área total es la suma de las áreas de los recintos.

La integral definida de la multiplicación de un número por una función

La integral definida de la multiplicación de un número por una función es igual a ese número por la integral definida de la función:

Es decir, podemos sacar la constante fuera de la integral al igual que hacemos en las integrales indefinidas.

Integrales definidas de dos funciones

Si una función g(x) es mayor o igual que otra función f(x), es decir, g(x) queda por encima de f(x), entonces, su integral definida también será mayor o igual:

Esto es así ya que el área que encierra la función g(x) será mayor que la que encierre la función f(x).

Cambio de límites de integración

Si intercambiamos los límites de integración, el valor de la integral definida cambia de signo:

Esta propiedad es muy útil para no operar con valores negativos de las integrales definidas.

Ejercicios resueltos de aplicación las propiedades de las integrales definidas

Ahora vamos a aplicar algunas de las propiedades que acabamos de explicar en la resolución de ejercicios.

Ejercicio 1

Calcula el área limitada entre la siguiente función y el eje x:

El área limitada por esta función y el eje x será el área que quede entre la función y los puntos de corte con el eje x, que a su vez serán los límites de integración.

Por tanto, lo primero que tenemos que hacer es calcular los puntos de corte de la función con el eje x.

La función corta con el eje x cuando es igual a cero, por lo que debemos igualar a cero la función y resolver la ecuación de segundo grado que resulta:

Cuyas soluciones son:

Por tanto, la función corta al eje x en los puntos x=-1 y x=2.

Si representamos la función nos queda:

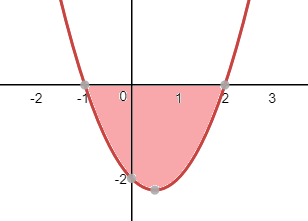
El área que tenemos que calcular queda por debajo del eje x, por lo que será igual a la integral de la función entre -1 y 2, y precedida por un signo menos:

Para eliminar el signo menos, le damos la vuelta a los límites de integración:

Ahora aplicamos la regla de Barrow.

Integramos la función y la dejamos entre corchetes con sus límites de integración:

Realizamos al resta de las funciones primitivas correspondientes sustituyendo la x por -1 y por 2 respectivamente::

Operamos, dejando el segundo paréntesis, ya que tiene delante un signo menos y no equivocarnos en los signos:

Y ahora sí, eliminamos el segundo paréntesis, cambiando de signo los términos que tiene dentro:

Finalmente, reducimos a común denominador y operamos hasta llegar al resultado final:

El área limitada entre la función y el eje x tiene un valor de 9/2 unidades cuadradas.

Ejercicio 2

Calcular el área limitada entre a siguiente función y el eje x:

Al igual que en el caso anterior, el área limitada por esta función y el eje x será el área que quede entre la función y los puntos de corte con el eje x.

Por tanto, vamos a calcular los puntos de corte de la función con el eje x.

La función corta con el eje x cuando es igual a cero, por lo que debemos igualar a cero la función y resolver la ecuación que nos queda:

En este caso nos queda una ecuación bicuadrada, que tiene 4 soluciones que son:

Por lo tanto, la función corta al eje x cuatro veces en los puntos -2, -1, 1 y 2, lo que quiere decir también que la función pasa de ser positiva a negativa y viceversa más de una vez.

Si la representamos nos queda de la siguiente manera:

El área de que tenemos que calcular está separada en 3 recintos, por lo que el área total será la suma de los 3 recientos:

El área limitada por la función y los puntos de corte -2 y -1 queda por debajo del eje x. Por tanto, será igual a menos la integral de la función entre -2 y -1, ya que la integral tiene un valor negativo:

Entre los puntos de corte -1 y 1, la función es positiva y el área a calcular queda por encima del eje x, por lo que se calcular como la integral de la función entre -1 y 1:

Por último, entre los puntos de corte x=1 y x=2, la función vuelve a ser negativa, por lo que el área queda por debajo del eje x. El área será igual a menos la integral de la función entre 1 y 2:

Vamos a ir resolviendo cada una de estas áreas.

Empezamos por S1:

Para que el valor de la integral sea positivo, en primer lugar le cambiamos el signo a la integral y e intercambiamos los límites de integración:

Integramos, dejando la primitiva entre corchetes con los límites:

Y aplicamos la regla de Barrow, realizando la resta del valor de la primitiva para x=-2 menos el valor de la primitiva para x=-1:

Y operamos hasta llegar al valor del área de S1:

S1 tiene una área de 22/15 unidades cudadradas.

Seguimos con S2:

Integramos:

Aplicamos la regla de Barrow:

Y operamos:

S2 tiene un área de 76/15 unidades cuadradas.

Por último, calculamos el área de S3:

Volvemos la integral positiva intercambiando los límites de integración:

Integramos:

Aplicamos la regla de Barrow:

Y operamos:

El área de S3 es 22/15 unidades cuadradas.

Calculamos el área total que es la suma de las áreas de cada reciento:

Por tanto, el área limitada entre la función y el eje x tiene un valor de 8 unidades cuadradas.

Si te das cuenta, S1 y S3 tiene el mismo valor, ya que la función es simétrica. Por tanto, no es necesario volver a calcular S3. Se puede justificar su valor diciendo que es simétrica a S1.

Ejercicio 3

Calcular el área limitada entre a siguiente función y el eje x y las rectas x=-4 y x=7:

Para entender mejor el área que nos piden en este ejercicio, representamos tanto la gráfica como las rectas:

El área que queda encerrada entre las rectas y la función, por encima del eje x es el área que nos están pidiendo, es decir, S1 y S2:

Vamos a calcular cada una de las áreas.

En primer lugar, calculamos los puntos de corte de la función con el eje x. Para ello igualamos la función a cero:

Y resolvemos la ecuación de segundo grado resultante:

Las soluciones son x=-3 y x=5:

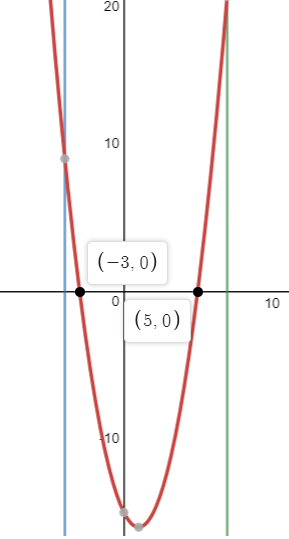
El área S1 la calculamos como la integral de la función entre los límites de integración x=-4 (corte de la recta y la función) y x=-3 (corte de la función y el eje x):

Integramos:

Aplicamos la regla de Barrow:

Y operamos:

Para calcular S2 hacemos lo mismo: la calculamos como la integral de la función entre los límites de integración x=5 (corte de la función y el eje x) y x=7 (corte de la recta y la función):