Operaciones con Fracciones Algebraicas.
Una expresión algebraica es una combinación de letras, números y signos de operaciones. Las letras suelen representar cantidades desconocidas y se denominan variables o incógnitas.
Las expresiones algebraicas nos permiten traducir al lenguaje matemático expresiones del lenguaje habitual.
Conceptos básicos que debes saber
Se llama: Término.Un Término separamos de otro, con los signos más o menos:
Un Término consta de dos partes: coeficiente y factor literal. Coeficiente: Es el número que va delante de las letras (si no lleva ninguna cifra, recuerda que lleva el 1).
Factor Literal: Es la compuesta por letras con sus exponentes, si los tienen.
Tipos de expresiones algebraicas
monomio
|
binomio
|
trinomio
|
3x
|
2x + 4
|
X2 + x + 5
|
Monomio: Se llama monomio a la expresión algebraica que tiene un solo término. Ejemplos de expresiones algebraicas de un solo término:
Binomio: Se llama binomio a la expresión algebraica que tiene dos términos. Ejemplos de expresiones algebraicas de dos términos:
Trinomio: Se llama trinomio a la expresión algebraica que tiene tres términos. Ejemplo:
Las expresiones algebraicas que contienen más de tres términos se llaman
Polinomios.
Una fracción algebraica es una expresión fraccionaria en la quenumerador y denominador son polinomios.Suma y resta de fracciones algebraicas:
10.1 Calcula el resultado de la suma:
1º Calculas el mínimo común múltiplo de los denominadores:
vemos que el m.c.m.(2, 3, 4) = 12
2º Divides el m.c.m. por cada denominador y el cociente lo multiplicas por el numerador:
10.2 Calcula el valor de:
Respuesta: 
Solución:
1º Calculamos el m.c.m.(3, 4 y 5) = 60
2º Dividimos 60 entre cada denominador y el cociente lo multiplicamos por su numerador y escribiendo por delante el signo que le corresponda.
10.3 Calcula la suma:
Respuesta: 
Solución:
Cuando tengas un término entero (sin denominador), si encuentras alguna dificultad le pones un 1 como denominador. Dividir o multiplicar un número por 1 es dejarle como está, pero a veces, resuelve alguna duda:
El m.c.m. de denominadores es 5. Cada denominador lo dividimos por este número y el cociente lo multiplicamos por su numerador.
10.4 Calcula:
Respuesta: 
10.5 Calcula:
Respuesta: 
Solución:
Trabajar con letras es muy sencillo. El m.c.m. de ‘a’ y ‘b’ es ‘ab’. Estas dos letras no tienen nada en común. Imagina que ‘a’ es igual a 7 y ‘b’ es igual a 5. Como 7 y 5 son primos, no tienen nada en común, el m.c.n.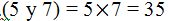 
lo mismo que el m.c.m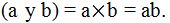 
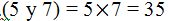lo mismo que el m.c.m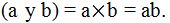
El m.c.m. de los denominadores dividimos por cada denominador y el cociente lo multiplicamos por su numerador:
Dividir 
es como dividir 
suponiendo que a = 7 y b = 5
es como dividir suponiendo que a = 7 y b = 5
Simplificamos los factores iguales en el numerador y denominador y nos quedarían:
10.6 Calcula:
Respuesta: 
Solución:
Este ejercicio puedes escribirlo:
El m.c.m. de los denominadores es xy
Dividimos este valor por cada denominador y el cociente multiplicamos por su numerador:
No se debe simplificar xy del numerador con el xy del denominador porque el del numerador está sumando y para simplificar los términos tienen que estar multiplicando.
10.7 Calcula la suma:
Respuesta: 
Solución:
El m.c.m. de los denominadores es ‘ab’. Lo dividimos por cada denominador y el cociente lo multiplicamos por su correspondiente numerador:
Vemos que el numerador es el cuadrado de la diferencia de dos números:
10.8 Calcula:
Respuesta: 
Solución:
El denominador para los dos sumandos será (x – y).
Al numerador 1 le multiplico por (x – y). Al segundo numerador le multiplico por 1 porque (x – y) entre sí mismo vale 1:
Solución:
Reduzco términos semejantes en el numerador:
_____________________________
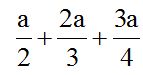
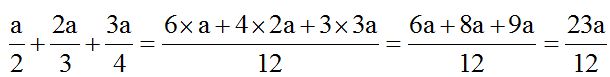
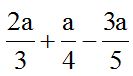
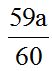
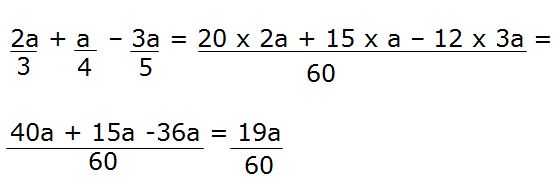
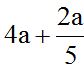
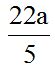
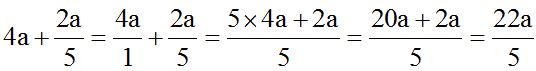
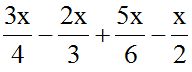
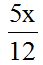
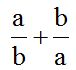
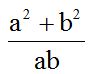
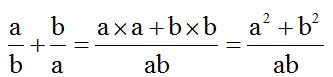
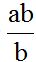
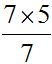
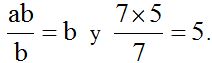
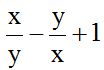
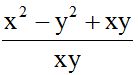
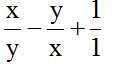
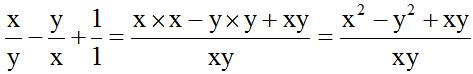
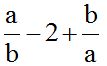
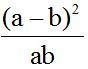
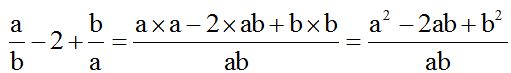
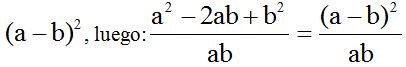
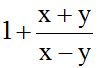
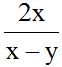
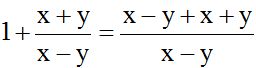
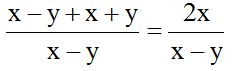
No hay comentarios.:
Publicar un comentario