Ecuaciones exponenciales (con logaritmos)
Contenido de esta página:
- Introducción
- Definición y propiedades del logaritmo
- 10 ecuaciones exponenciales resueltas (aplicando logaritmos)
- Enlace: Ecuaciones exponenciales (sin aplicar logaritmos)
1. Introducción
En algunas ecuaciones exponenciales es necesaria la aplicación de logaritmos para poder resolverlas. Esto ocurre básicamente cuando las exponenciales no tienen la misma base. Por ejemplo, la solución de la ecuación es
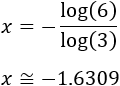 En esta página vamos a resolver 10 ecuaciones de este tipo. Para comprender los pasos se necesita conocer la definición y las propiedades de los logaritmos que damos a continuación.
En esta página vamos a resolver 10 ecuaciones de este tipo. Para comprender los pasos se necesita conocer la definición y las propiedades de los logaritmos que damos a continuación.
Nota: no calcularemos las soluciones complejas.
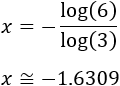
Nota: no calcularemos las soluciones complejas.
2. Definición y propiedades del logaritmo
El logaritmo en base del número positivo se denota por y su valor es el número al que se debe elevar la base del logaritmo, , para obtener el número . Es decir,
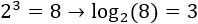
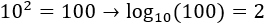
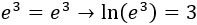 Las propiedades de los logaritmos son las siguientes:
Las propiedades de los logaritmos son las siguientes:
*La tercera propiedad es principalmente la que facilita la resolución de las ecuaciones exponenciales puesto que permite escribir la incógnita (que está en el exponente) como un factor que multiplica a un número (al logaritmo).
Enlace: demostraciones de las propiedades (final de la página).
Ejmplos:
- el logaritmo en base 2 de 8 es 3 porque 2 al cubo es 8:
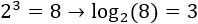
- el logaritmo en base 10 de 100 es 2 ya que 10 al cuadrado es 100:
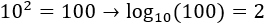
- el logaritmo en base (logaritmo natural, ) de es 3 ya que al cubo es :
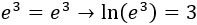
Logaritmo del producto:
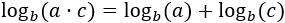 |
Logaritmo del cociente:
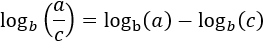 |
*Logaritmo de la potencia:
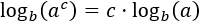 |
Cambio de base:
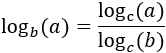 |
Propiedad útil en la práctica:
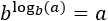 |
Enlace: demostraciones de las propiedades (final de la página).
3. 10 Ecuaciones resueltas
Como cada autor emplea una notación, en cada ecuación indicaremos la base del logaritmo que aplicamos para evitar las confusiones. Asimismo, aproximaremos las soluciones para que sea más rápido comprobarlas si se han utilizado logaritmos en bases distintas.
Las primeras ecuaciones las explicaremos más detalladamente.
Ecuación 1
Resolver con logaritmos en base 10:
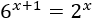
Solución
Escribiremos el logaritmo en base 10 sin indicar explícitamente la base (es lo habitual).
Aplicamos logaritmos en base 10:
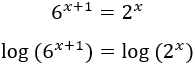 Escribimos los exponentes fuera de los logaritmos (multiplicando):
Escribimos los exponentes fuera de los logaritmos (multiplicando):
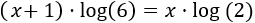 Calculamos los productos:
Calculamos los productos:
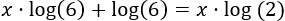 Escribimos en el lado izquierdo los elementos en los que aparece la incógnita y los otros en el lado derecho:
Escribimos en el lado izquierdo los elementos en los que aparece la incógnita y los otros en el lado derecho:
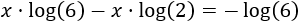 Extraemos el factor común en el lado izquierdo:
Extraemos el factor común en el lado izquierdo:
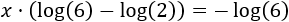 Aplicamos la propiedad de la resta de logaritmos:
Aplicamos la propiedad de la resta de logaritmos:
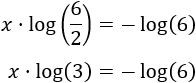 Finalmente, aislamos la incógnita:
Finalmente, aislamos la incógnita:
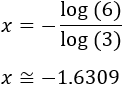
Aplicamos logaritmos en base 10:
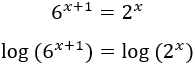
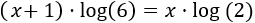
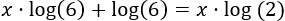
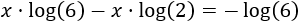
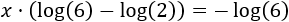
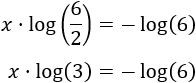
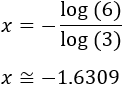
Ecuación 2
La siguiente ecuación se puede resolver sin aplicar logaritmos, pero se pide resolver con logaritmos en base 3:
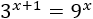
Solución
Aplicamos logaritmos en base 3:
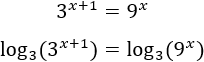 Escribimos los exponentes fuera de los logaritmos:
Escribimos los exponentes fuera de los logaritmos:
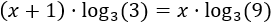 Calculamos los logaritmos:
Calculamos los logaritmos:
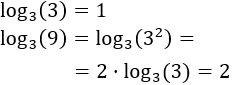 Por tanto, la ecuación queda como
Por tanto, la ecuación queda como
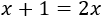 Y la solución es
Y la solución es
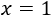
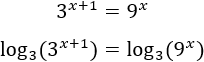
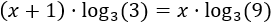
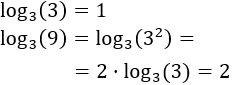
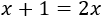
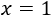
Ecuación 3
Resolver aplicando logaritmos en base 10:
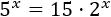
Solución
Aplicamos logaritmos de base 10:
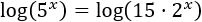 El logaritmo del lado derecho podemos escribirlo como una suma:
El logaritmo del lado derecho podemos escribirlo como una suma:
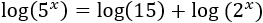 Extraemos los exponentes de los logaritmos:
Extraemos los exponentes de los logaritmos:
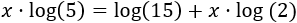 Escribimos en el lado izquierdo los sumandos que tienen la incógnita:
Escribimos en el lado izquierdo los sumandos que tienen la incógnita:
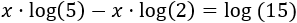 Finalmente, extraemos factor común y despejamos la incógnita:
Finalmente, extraemos factor común y despejamos la incógnita:
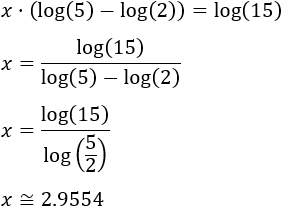
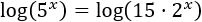
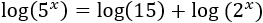
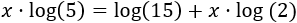
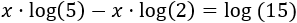
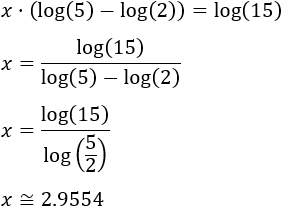
Ecuación 4
Resolver aplicando el cambio de variable y logaritmos en base 5:
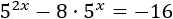
Solución
No podemos resolver la ecuación aplicando logaritmos directamente porque tendríamos una resta en el argumento:
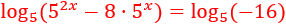 Las propiedades de los logaritmos no permiten simplificar el logaritmo de la izquierda. Además, en la derecha tenemos un argumento negativo.
Las propiedades de los logaritmos no permiten simplificar el logaritmo de la izquierda. Además, en la derecha tenemos un argumento negativo.
Si aplicamos el cambio de variable , entonces queda como
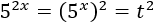 Con lo que la ecuación resultante es
Con lo que la ecuación resultante es
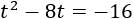 Es una ecuación de segundo grado cuya única solución es .
Es una ecuación de segundo grado cuya única solución es .
Deshacemos el cambio de variable:
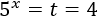 Aplicamos logaritmos en base 5 para resolver la ecuación exponencial que hemos obtenido:
Aplicamos logaritmos en base 5 para resolver la ecuación exponencial que hemos obtenido:
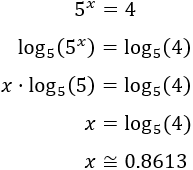
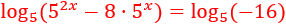
Si aplicamos el cambio de variable , entonces queda como
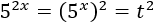
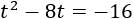
Deshacemos el cambio de variable:
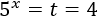
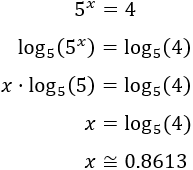
Ecuación 5
Resolver mediante logaritmos en base 3:
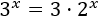
Solución
Aplicamos directamente logaritmos en base 3:
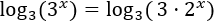 El logaritmo de la derecha puede escribirse como una suma:
El logaritmo de la derecha puede escribirse como una suma:
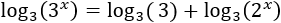 Escribimos los exponentes fuera de los logaritmos:
Escribimos los exponentes fuera de los logaritmos:
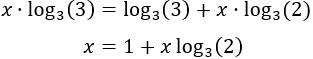 Aislamos la incógnita:
Aislamos la incógnita:
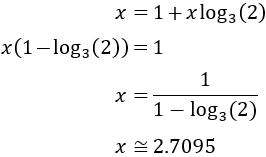
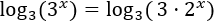
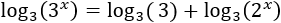
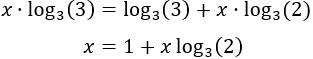
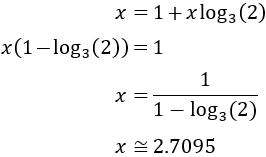
Ecuación 6
Resolver aplicando logaritmos en base decimal (base 10):
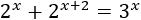
Solución
Simplificamos la ecuación antes de aplicar logaritmos. El segundo sumando de la izquierda puede escribirse como
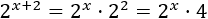 Operamos un poco en la ecuación:
Operamos un poco en la ecuación:
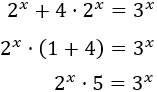 Aplicamos logaritmos en base decimal:
Aplicamos logaritmos en base decimal:
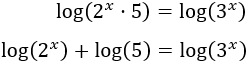 Operando de forma similar a las ecuaciones anteriores,
Operando de forma similar a las ecuaciones anteriores,
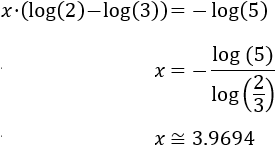
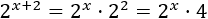
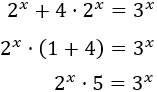
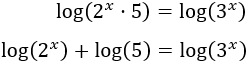
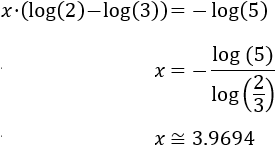
Ecuación 7
Escribir la siguiente ecuación como una ecuación exponencial para resolverla mediante logaritmos en base decimal:
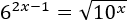
Solución
Ecuación 8
Resolver mediante el cambio de variable y aplicando logaritmos en base binaria (base 2):
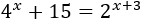
Solución
Ecuación 9
Resolver mediante logaritmos naturales (logaritmos en base , ):
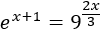
Solución
No hay comentarios.:
Publicar un comentario