Ecuaciones exponenciales
Descargar Folleto de estudio
Contenido de esta página:
- Breve Introducción
- Recordatorio de las propiedades de las potencias
- 25 ecuaciones exponenciales resueltas (sin aplicar logaritmos)
1. Introducción
Una ecuación exponencial es aquella en la que aparecen exponenciales, es decir, potencias cuyos exponentes son expresiones en las que aparece la incógnita, x. En esta sección resolveremos ecuaciones exponenciales sin usar logaritmos.
El método de resolución consiste en conseguir una igualdad de exponenciales con la misma base para poder igualar los exponentes. Por ejemplo:
La ecuación anterior se cumple si los exponentes son iguales. Por tanto, en este ejemplo el valor que debe tomar x es 3.
Para conseguir igualdades como la anterior, tendremos que factorizar, expresar los números en forma de potencias, aplicar las propiedades de las potencias y escribir las raíces como potencias. En ocasiones, tendremos que realizar un cambio de variable para transformar la ecuación en una ecuación de primer o de segundo grado e, incluso, de grado mayor.
También se pueden resolver aplicando logaritmos, pero nosotros dejaremos este procedimiento para ecuaciones con mayor dificultad en las que las exponenciales tienen bases distintas y, por tanto, no podemos usar la técnica anterior de igualar exponentes. Por ejemplo, en la siguiente ecuación las bases son distintas (coprimas)
y su solución (real) es, aplicando logaritmos,
El método de resolución consiste en conseguir una igualdad de exponenciales con la misma base para poder igualar los exponentes. Por ejemplo:
La ecuación anterior se cumple si los exponentes son iguales. Por tanto, en este ejemplo el valor que debe tomar x es 3.
Para conseguir igualdades como la anterior, tendremos que factorizar, expresar los números en forma de potencias, aplicar las propiedades de las potencias y escribir las raíces como potencias. En ocasiones, tendremos que realizar un cambio de variable para transformar la ecuación en una ecuación de primer o de segundo grado e, incluso, de grado mayor.
También se pueden resolver aplicando logaritmos, pero nosotros dejaremos este procedimiento para ecuaciones con mayor dificultad en las que las exponenciales tienen bases distintas y, por tanto, no podemos usar la técnica anterior de igualar exponentes. Por ejemplo, en la siguiente ecuación las bases son distintas (coprimas)
y su solución (real) es, aplicando logaritmos,
2. Propiedades de las potencias
Como una exponencial es realmente una potencia con una o varias incógnitas en el exponente, podemos utilizar las propiedades de las potencias para trabajar con las exponenciales.
Esto nos permite simplificar las ecuaciones exponenciales o escribirlas en una forma que facilite su resolución.
Las propiedades de las potencias son las siguientes:
Esto nos permite simplificar las ecuaciones exponenciales o escribirlas en una forma que facilite su resolución.
Las propiedades de las potencias son las siguientes:
Producto (misma base)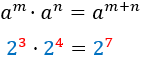 | Potencia (de potencia)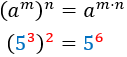 |
Cociente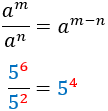 | Exponente negativo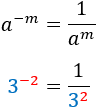 |
Inverso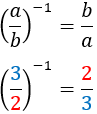 | Inverso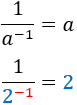 |
3. 25 Ecuaciones resueltas
En esta sección resolvemos 25 ecuaciones exponenciales de forma directa, aplicando las propiedades de las potencias y/o aplicando un cambio de variable.
No resolvemos ninguna ecuación aplicando logaritmos. Podemos encontrar ejemplos de este método de resolución en ecuaciones exponenciales explicadas (PyE).
Ecuación 1
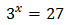
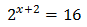
Ecuación 3
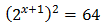
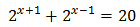
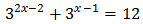
Ecuación 6
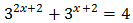
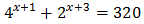
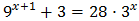
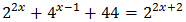
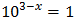
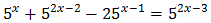
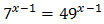
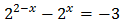
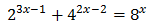
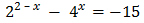
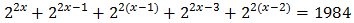
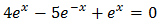
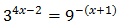
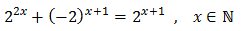
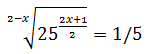
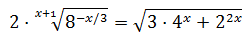
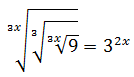
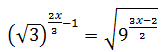
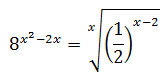
No resolvemos ninguna ecuación aplicando logaritmos. Podemos encontrar ejemplos de este método de resolución en ecuaciones exponenciales explicadas (PyE).
Ecuación 1
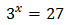
Ver solución
Podemos escribir 27 como la potencia . De este modo, la ecuación queda como
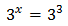 Tenemos una igualdad entre dos potencias con la misma base. Para que la igualdad sea cierta, ambas potencias deben tener el mismo exponente:
Tenemos una igualdad entre dos potencias con la misma base. Para que la igualdad sea cierta, ambas potencias deben tener el mismo exponente:
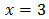
Ecuación 2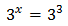
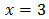
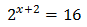
Ver solución
Escribimos 16 como una potencia de 2:
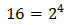 Podemos reescribir la ecuación como
Podemos reescribir la ecuación como
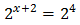 Por tanto, igualando los exponentes,
Por tanto, igualando los exponentes,
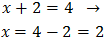 Luego la solución de la ecuación exponencial es .
Luego la solución de la ecuación exponencial es .
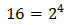
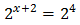
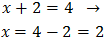
Ecuación 3
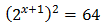
Ver solución
Escribimos 64 como una potencia de 2:
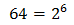 Operamos en la ecuación usando las propiedades de las potencias
Operamos en la ecuación usando las propiedades de las potencias
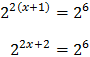 Por tanto, obtenemos una ecuación de primer grado:
Por tanto, obtenemos una ecuación de primer grado:
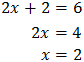
Ecuación 4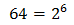
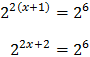
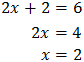
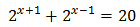
Ver solución
Aplicando las propiedades de las potencias,
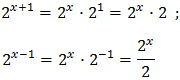 Con lo que podemos reescribir la ecuación como
Con lo que podemos reescribir la ecuación como
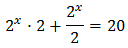 De este modo podemos extraer factor común de :
De este modo podemos extraer factor común de :
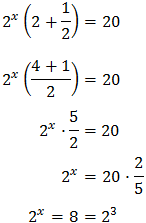 Es decir, la solución es .
Es decir, la solución es .
Ecuación 5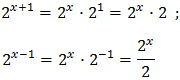
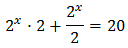
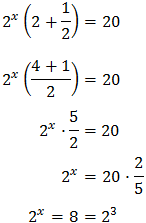
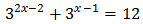
Ver solución
Reescribimos los sumandos de la ecuación:
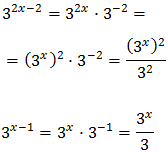 Luego podemos reescribir la ecuación como
Luego podemos reescribir la ecuación como
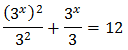 Tal y como está escrita la ecuación, podemos considerar la base común . Como una de estas potencias está al cuadrado, aplicamos el cambio de variable siguiente
Tal y como está escrita la ecuación, podemos considerar la base común . Como una de estas potencias está al cuadrado, aplicamos el cambio de variable siguiente
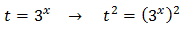 Sustituyendo en la ecuación obtenemos
Sustituyendo en la ecuación obtenemos
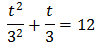 Es decir, una ecuación de segundo grado
Es decir, una ecuación de segundo grado
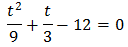 Multiplicamos por 9 la ecuación para simplificarla:
Multiplicamos por 9 la ecuación para simplificarla:
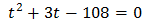 Las soluciones de esta ecuación son:
Las soluciones de esta ecuación son:
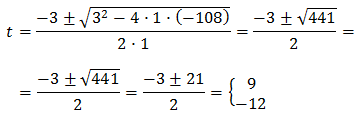 Por tanto, tenemos que
Por tanto, tenemos que
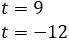 Al deshacer el cambio de variable,
Al deshacer el cambio de variable,
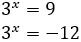 La segunda opción no es posible porque es negativa (las potencias de 3 no pueden ser negativas). Por tanto, la única solución, , de la ecuación exponencial debe cumplir
La segunda opción no es posible porque es negativa (las potencias de 3 no pueden ser negativas). Por tanto, la única solución, , de la ecuación exponencial debe cumplir
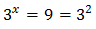 De donde obtenemos
De donde obtenemos
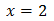
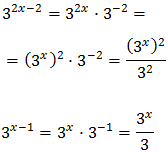
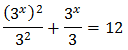
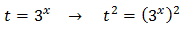
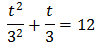
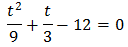
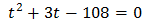
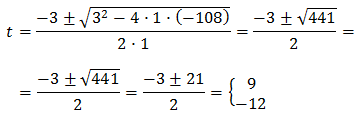
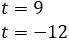
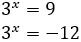
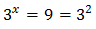
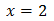
Ecuación 6
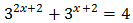
Ver solución
Reescribimos los sumandos:
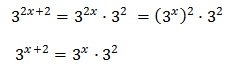 Con lo que podemos reescribir la ecuación como
Con lo que podemos reescribir la ecuación como
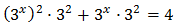 Sea el cambio de variable
Sea el cambio de variable
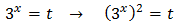 Sustituyendo en la ecuación obtenemos una ecuación de segundo grado
Sustituyendo en la ecuación obtenemos una ecuación de segundo grado
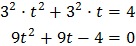 cuyas soluciones son
cuyas soluciones son
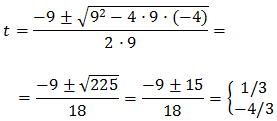 Por tanto, tenemos que
Por tanto, tenemos que
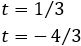 Al deshacer el cambio de variable,
Al deshacer el cambio de variable,
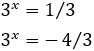 La segunda solución no es posible porque es negativa, pero la primera sí. Luego debe cumplirse
La segunda solución no es posible porque es negativa, pero la primera sí. Luego debe cumplirse
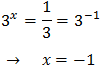 Por tanto, la solución de la ecuación exponencial es .
Por tanto, la solución de la ecuación exponencial es .
Ecuación 7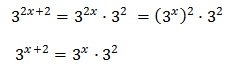
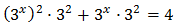
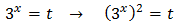
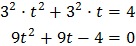
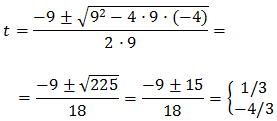
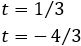
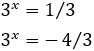
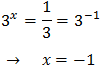
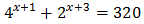
Ver solución
Operamos para tener potencias con la misma base:
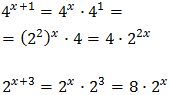 Con lo que podemos reescribir la ecuación como
Con lo que podemos reescribir la ecuación como
 Aplicamos un cambio de variable:
Aplicamos un cambio de variable:
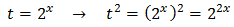 Substituimos y obtenemos la ecuación de segundo grado
Substituimos y obtenemos la ecuación de segundo grado
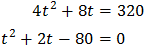 cuyas soluciones son
cuyas soluciones son
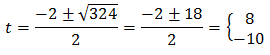 Por tanto,
Por tanto,
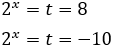 La segunda solución no es posible por ser negtiva. Por tanto,
La segunda solución no es posible por ser negtiva. Por tanto,
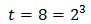 Es decir, debe cumplirse
Es decir, debe cumplirse
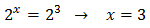
Ecuación 8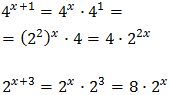

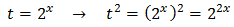
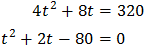
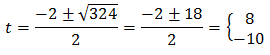
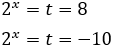
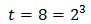
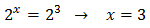
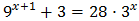
Ver solución
Escribimos como una potencia de base 3:
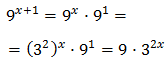 Con lo que podemos reescribir la ecuación como
Con lo que podemos reescribir la ecuación como
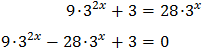 Llamamos
Llamamos
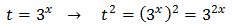 Substituimos y obtenemos la ecuación de segundo grado
Substituimos y obtenemos la ecuación de segundo grado
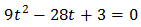 La resolvemos
La resolvemos
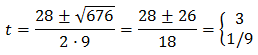 Por tanto,
Por tanto,
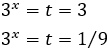 Notemos que
Notemos que
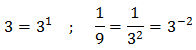 Con lo que ambas son potencias de 3. Luego la ecuación exponencial tiene dos soluciones y son
Con lo que ambas son potencias de 3. Luego la ecuación exponencial tiene dos soluciones y son
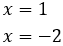
Ecuación 9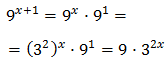
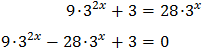
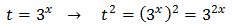
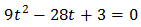
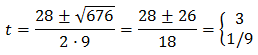
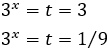
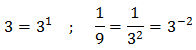
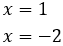
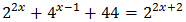
Ver solución
Escribimos las exponenciales como potencias de base 2:
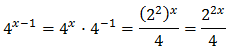
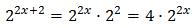 Con lo que podemos reescribir la ecuación como
Con lo que podemos reescribir la ecuación como
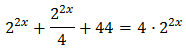 Llamamos
Llamamos
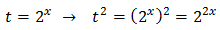 Substituimos en la ecuación exponencial y obtenemos la ecuación de segundo grado
Substituimos en la ecuación exponencial y obtenemos la ecuación de segundo grado
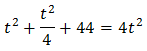 Resolvemos
Resolvemos
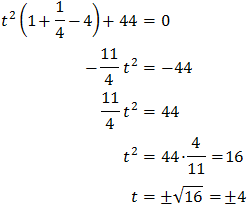 Por tanto, como ,
Por tanto, como ,
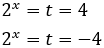 Las soluciones y no son posibles por ser una cero y la otra negativa. Luego la única solución solución es
Las soluciones y no son posibles por ser una cero y la otra negativa. Luego la única solución solución es
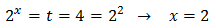
Ecuación 10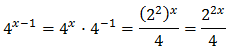
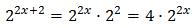
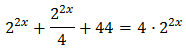
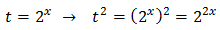
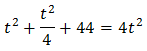
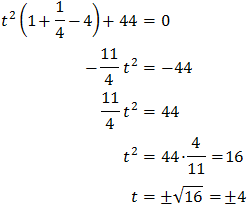
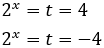
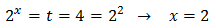
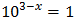
Ver solución
Podemos escribir 1 como una potencia de 10:
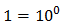 Con lo que podemos reescribir la ecuación como
Con lo que podemos reescribir la ecuación como
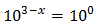 Por tanto, debe cumplirse
Por tanto, debe cumplirse
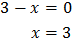
Ecuación 11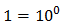
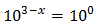
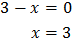
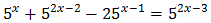
Ver solución
Ecuación 12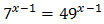
Ver solución
Ecuación 13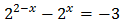
Ver solución
Ecuación 14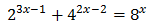
Ver solución
Ecuación 15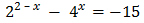
Ver solución
Ecuación 16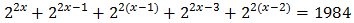
Ver solución
Ecuación 17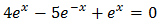
Ver solución
Ecuación 18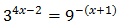
Ver solución
Ecuación 19 (dificultad alta)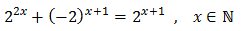
Ver solución
Ecuación 20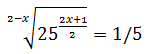
Ver solución
Ecuación 21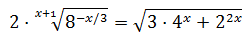
Ver solución
Ecuación 22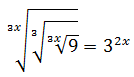
Ver solución
Ecuación 23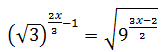
Ver solución
Ecuación 24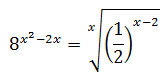
Ver solución
No hay comentarios.:
Publicar un comentario