Criterio de la primera

 

Extremos relativos. Criterios de la 1ra derivada

Encontrar extremos relativos (criterio de la primera derivada)

El criterio de la primera derivada es el proceso de analizar funciones utilizando sus primeras derivadas en búsqueda de puntos extremos. Este trabajo involucra múltiples pasos, por lo que necesitamos descomprimirlo en una forma que nos ayude a evitar errores u omisiones perjudiciales.

PASOS

1. - Obtener el valor de la derivada de la función

2. - Igualar a cero la ecuación que resulta.

3. - Resolver la ecuación para hallar el valor crítico de x.

4. - Sustituir el valor crítico de x en la función dada y encontrar el valor de f(x).

5. - Tomar un valor ligeramente mayor y otro ligeramente menor que el valor crítico de x y sustituir en la derivada de la función.

6. - Si la pendiente resulta con un valor (+)  a (-) entonces, se trata de un máximo, y si cambia de (-) a (+) entonces es un mínimo.

Ejemplo 1: Encontrar el valor máximo o mínimo de la función  y = 4x – x²

Siguiendo los tres pasos anteriores, tenemos

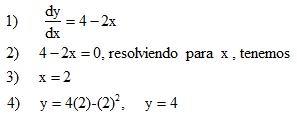
Tomar dos valores, uno ligeramente mayor y otro ligeramente menor que x = 2

Para x = 1.9   dy/dx = 4 – 2 (1.9) = 0.2    es positivo

Para x = 2.1    dy/dx  = 4 – 2 (2.1) = -0. 2  es negativo

 

Se observa que hay un cambio en la pendiente de la recta de (+) a (-) entonces 

la curva pasa de creciente a decreciente por lo que se deduce que la curva presenta un punto máximo.

 

Ejemplo 2:  Determinar si la gráfica de la función y = x² – 3x + 6 presenta un máximo o un mínimo,

 mediante el método de la derivada.

Siguiendo el procedimiento anterior

 

1)                   dy/dx = 2x – 3

 

2)                    2x – 3 = 0,  donde x = 3/2 = 1.5

 

3)                    Tomar dos valores cercanos a x = 3/2

 

Para x = 1    dy/dx = 2(1) – 3 = 3 – 2 = -1   es negativo

Para x = 2    dy/dx = 2(2) – 3 =  4 – 3 = 0   es positivo

 

La gráfica va de negativo a positivo, entonces la gráfica presenta un valor mínimo; va de decreciente a creciente.

 

Para conocer la coordenada en y del valor mínimo; sustituimos x  = 3/2 en la función:

y = (3/2)² – 3(3/2) + 6, de donde y = 15/4

OTRO Ejemplo

 Encontrar los puntos extremos relativos de $f(x)=\dfrac{x^2}{x-1}$f, left parenthesis, x, right parenthesis, equals, start fraction, x, squared, divided by, x, minus, 1, end fraction

Paso 1: encontrar $f'(x)$f, prime, left parenthesis, x, right parenthesis

Para encontrar los puntos extremos relativos de $f$f, debemos usar $f'$f, prime. Así que empezamos derivando $f$f:

$f'(x)=\dfrac{x^2-2x}{(x-1)^2}$f, prime, left parenthesis, x, right parenthesis, equals, start fraction, x, squared, minus, 2, x, divided by, left parenthesis, x, minus, 1, right parenthesis, squared, end fraction

Paso 2: encontrar todos los puntos críticos y los puntos donde $f$f no está definida.

Los puntos críticos de una función $f$f son los valores de $x$x en el dominio de $f$f para los cuales $f'(x)=0$f, prime, left parenthesis, x, right parenthesis, equals, 0 o donde $f'$f, prime no está definida. Además de esos, debemos buscar puntos donde la función $f$f no está definida.

Lo importante de estos puntos es que el signo de $f'$f, prime debe ser el mismo entre dos puntos consecutivos.

En nuestro caso, los puntos son $x=0$x, equals, 0, $x=1$x, equals, 1 y $x=2$x, equals, 2.

Paso 3: analizar intervalos crecientes o decrecientes

Esto puede hacerse de muchas maneras, pero nos gusta hacerlo con un diagrama de signos. En un diagrama de signos, seleccionamos un valor de prueba en cada intervalo que está acotado por los puntos encontrados en el Paso 2 y verificamos el signo de la derivada en ese valor.

Este es el diagrama de signos para nuestra función:

Intervalo	Valor $x$x de prueba	$f'(x)$f, prime, left parenthesis, x, right parenthesis	Conclusión
$(-\infty,0)$left parenthesis, minus, infinity, comma, 0, right parenthesis	$x=-1$x, equals, minus, 1	$f'(-1)=0.75>0$f, prime, left parenthesis, minus, 1, right parenthesis, equals, 0, point, 75, is greater than, 0	$f$f es creciente $\nearrow$\nearrow
$(0,1)$left parenthesis, 0, comma, 1, right parenthesis	$x=0.5$x, equals, 0, point, 5	$f'(0.5)=-3<0$f, prime, left parenthesis, 0, point, 5, right parenthesis, equals, minus, 3, is less than, 0	$f$f es decreciente $\searrow$\searrow
$(1,2)$left parenthesis, 1, comma, 2, right parenthesis	$x=1.5$x, equals, 1, point, 5	$f'(1.5)=-3<0$f, prime, left parenthesis, 1, point, 5, right parenthesis, equals, minus, 3, is less than, 0	$f$f es decreciente $\searrow$\searrow
$(2,\infty)$left parenthesis, 2, comma, infinity, right parenthesis	$x=3$x, equals, 3	$f'(3)=0.75>0$f, prime, left parenthesis, 3, right parenthesis, equals, 0, point, 75, is greater than, 0	$f$f es creciente $\nearrow$\nearrow

Paso 4: encontrar puntos extremos

Ahora que sabemos los intervalos donde $f$f crece o decrece, podemos encontrar sus puntos extremos. Un punto extremo podría ser aquel donde $f$f está definida y $f'$f, prime cambia de signo.

En nuestro caso:

• $f$f crece antes de $x=0$x, equals, 0, decrece después, y está definida en $x=0$x, equals, 0. Así que $f$f tiene un punto máximo local en $x=0$x, equals, 0.
• $f$f decrece antes de $x=2$x, equals, 2, crece después, y está definida en $x=2$x, equals, 2. Así que $f$f tiene un punto mínimo local en $x=2$x, equals, 2.
• $f$f está indefinida en $x=1$x, equals, 1, así que ahí no tiene un punto extremo.