Coeficiente de correlación lineal

En una distribución bidimensional puede ocurrir que las dos variables guarden algún tipo de relación entre si.

Por ejemplo, si se analiza la estatura y el peso de los alumnos de una clase es muy posible que exista relación entre ambas variables: mientras más alto sea el alumno, mayor será su peso.

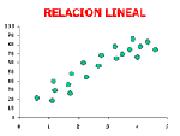
El coeficiente de correlación lineal mide el grado de intensidad de esta posible relación entre las variables. Este coeficiente se aplica cuando la relación que puede existir entre las variables es lineal (es decir, si representáramos en un gráfico los pares de valores de las dos variables la nube de puntos se aproximaría a una recta).

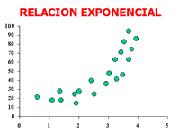
No obstante, puede que exista una relación que no sea lineal, sino exponencial, parabólica, etc. En estos casos, el coeficiente de correlación lineal mediría mal la intensidad de la relación las variables, por lo que convendría utilizar otro tipo de coeficiente más apropiado.

Para ver, por tanto, si se puede utilizar el coeficiente de correlación lineal, lo mejor es representar los pares de valores en un gráfico y ver que forma describen.

El coeficiente de correlación lineal se calcula aplicando la siguiente fórmula:

Es decir:

Numerador: se denomina covarianza y se calcula de la siguiente manera: en cada par de valores (x,y) se multiplica la "x" menos su media, por la "y" menos su media. Se suma el resultado obtenido de todos los pares de valores y este resultado se divide por el tamaño de la muestra.

Denominador se calcula el producto de las varianzas de "x" y de "y", y a este producto se le calcula la raíz cuadrada.

Los valores que puede tomar el coeficiente de correlación "r" son: -1 < r < 1

Si "r" > 0, la correlación lineal es positiva (si sube el valor de una variable sube el de la otra). La correlación es tanto más fuerte cuanto más se aproxime a 1.

Por ejemplo: altura y peso: los alumnos más altos suelen pesar más.

Si "r" < 0, la correlación lineal es negativa (si sube el valor de una variable disminuye el de la otra). La correlación negativa es tanto más fuerte cuanto más se aproxime a -1.

Por ejemplo: peso y velocidad: los alumnos más gordos suelen correr menos.

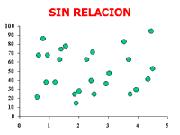
Si "r" = 0, no existe correlación lineal entre las variables. Aunque podría existir otro tipo de correlación (parabólica, exponencial, etc.)

De todos modos, aunque el valor de "r" fuera próximo a 1 o -1, tampoco esto quiere decir obligatoriamente que existe una relación de causa-efecto entre las dos variables, ya que este resultado podría haberse debido al puro azar.

Ejemplo: vamos a calcular el coeficiente de correlación de la siguiente serie de datos de altura y peso de los alumnos de una clase:

Alumno	Estatura	Peso	Alumno	Estatura	Peso	Alumno	Estatura	Peso
x	x	x	x	x	x	x	x	x
Alumno 1	1,25	32	Alumno 11	1,25	33	Alumno 21	1,25	33
Alumno 2	1,28	33	Alumno 12	1,28	35	Alumno 22	1,28	34
Alumno 3	1,27	34	Alumno 13	1,27	34	Alumno 23	1,27	34
Alumno 4	1,21	30	Alumno 14	1,21	30	Alumno 24	1,21	31
Alumno 5	1,22	32	Alumno 15	1,22	33	Alumno 25	1,22	32
Alumno 6	1,29	35	Alumno 16	1,29	34	Alumno 26	1,29	34
Alumno 7	1,30	34	Alumno 17	1,30	35	Alumno 27	1,30	34
Alumno 8	1,24	32	Alumno 18	1,24	32	Alumno 28	1,24	31
Alumno 9	1,27	32	Alumno 19	1,27	33	Alumno 29	1,27	35
Alumno 10	1,29	35	Alumno 20	1,29	33	Alumno 30	1,29	34

Aplicamos la fórmula:

(1/30) * (0,826)

r =-----------------------------------------------------------

(((1/30)*(0,02568)) * ((1/30)*(51,366)))^(1/2)

Luego,

r = 0,719

Por lo tanto, la correlación existente entre estas dos variables es elevada (0,7) y de signo positivo.

EJEMPLO |1

1 Una compañía desea hacer predicciones del valor anual de sus ventas totales en cierto país a partir de la relación de éstas y la renta nacional. Para investigar la relación cuenta con los siguientes datos:

$\begin{matrix} \hline \textup{X} & \textup{Y}\\ \hline 189 & 402 \\ 190 & 404 \\ 208 & 412 \\ 227 & 425 \\ 239 & 429 \\ 252 & 436 \\ 257 & 440 \\ 274 & 447 \\ 293 & 458 \\ 308 & 469 \\ 316 & 469 \\ \hline \end{matrix}$

X representa la renta nacional en millones de euros e Y representa las ventas de la compañía en miles de euros en el periodo que va desde $1990$ hasta $2000$ (ambos inclusive). Calcular:

1La recta de regresión de Y sobre X.

2El coeficiente de correlación lineal e interpretarlo.

3Si en $2001$ la renta nacional del país fue de $325$ millones de euros. ¿Cuál será la predicción para las ventas de la compañía en este año?

X representa la renta nacional en millones de euros e Y representa las ventas de la compañía en miles de euros en el periodo que va desde $1990$ hasta $2000$ (ambos inclusive). Calcular:

1 La recta de regresión de Y sobre X.

$\begin{matrix} \hline & \textup{X}_{i} & \textup{Y}_{i} & \textup{X}_{i}^{2} & \textup{Y}_{i}^{2} & \textup{X}_{i}\cdot \textup{Y}_{i}\\ \hline & 189 & 402 & 35721 & 161604 & 75978\\ & 190 & 404 & 36100 & 163216 & 76760\\ & 208 & 412 & 43264 & 169744 & 85696\\ & 227 & 425 & 51529 & 180625 & 96475\\ & 239 & 429 & 57121 & 184041 & 102531\\ & 252 & 436 & 63504 & 190096 & 109872\\ & 257 & 440 & 66049 & 193600 & 113080\\ & 274 & 447 & 75076 & 199809 & 122478\\ & 293 & 458 & 85849 & 209764 & 134194\\ & 308 & 469 & 94864 & 219961 & 144452\\ & 316 & 469 & 99856 & 219961 & 148204\\ \sum & 2753 & 4791 & 708933 & 2092421 & 1209720 \\ \hline \end{matrix}$

$\bar{x}=\cfrac{2753}{11}=250.27$

$\bar{y}=\cfrac{4791}{11}=435.55$

$\sigma _{x}^{2}=\cfrac{708933}{11}-250.27^{2}=1813.38$

$\sigma _{y}^{2}=\cfrac{2092421}{11}-435.55^{2}=516.29$

$\sigma _{x}=\sqrt{1813.38}=42.58$

$\sigma _{y}=\sqrt{516.29}=22.72$

$\sigma _{xy}=\cfrac{1209720}{11}-250.27\cdot 435.55=469.45$

$y-435.55=0.53(x-250.27)\; \; \; \; \; \Rightarrow \; \; \; \; \; y=0.53+302.91$

2 El coeficiente de correlación lineal e interpretarlo.

$r=\cfrac{469.45}{42.58\cdot 22.81}=0.998$

Es un coeficiente de correlación positivo y cercano a uno, por lo que la correlación es directa y fuerte.

3 Si en $2001$ la renta nacional del país fue de $325$ millones de euros. ¿Cuál será la predicción para las ventas de la compañía en este año?

$y=0.53\cdot 325+302.91=475.16$

EJEMPLO 2

2 La información estadística obtenida de una muestra de tamaño 12 sobre la relación existente entre la inversión realizada y el rendimiento obtenido en cientos de miles de euros para explotaciones agrícolas, se muestra en el siguiente cuadro: Inversión (X), Rendimiento (Y)

$\begin{matrix} \hline \textup{X} & \textup{Y}\\ \hline 11 & 2\\ 14 & 3\\ 16 & 5\\ 15 & 6\\ 16 & 5\\ 18 & 3\\ 20 & 7\\ 21 & 10\\ 14 & 6\\ 20 & 10\\ 19 & 5\\ 11 & 6\\ \hline \end{matrix}$

Calcular:

1La recta de regresión del rendimiento respecto de la inversión.

2La previsión de inversión que se obtendrá con un rendimiento de 1 250 000 €.

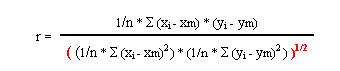
La información estadística obtenida de una muestra de tamaño 12 sobre la relación existente entre la inversión realizada y el rendimiento obtenido en cientos de miles de euros para explotaciones agrícolas, se muestra en el siguiente cuadro:

$\begin{matrix} \hline \textup{X} & \textup{Y}\\ \hline 11 & 2\\ 14 & 3\\ 16 & 5\\ 15 & 6\\ 16 & 5\\ 18 & 3\\ 20 & 7\\ 21 & 10\\ 14 & 6\\ 20 & 10\\ 19 & 5\\ 11 & 6\\ \hline \end{matrix}$

Calcular:

1 La recta de regresión del rendimiento respecto de la inversión.

$\begin{matrix} \hline &\textup{X}_{i} & \textup{Y}_{i} & \textup{X}^{2}_{i} & \textup{Y}^{2}_{i} & \textup{X}_{i}^{2}\cdot \textup{Y}_{i}^{2}\\ \hline &11 & 2 & 121 & 4 & 22\\ &14 & 3 & 196 & 9 & 42\\ &16 & 5 & 256 & 25 & 80\\ &15 & 6 & 225 & 36 & 90\\ &16 & 5 & 256 & 25 & 80\\ &18 & 3 & 324 & 9 & 54\\ &20 & 7 & 400 & 49 & 140\\ &21 & 10 & 441 & 100 & 210\\ &14 & 6 & 196 & 36 & 84\\ &20 & 10 & 400 & 100 & 200\\ &19 & 5 & 361 & 25 & 95\\ &11 & 6 & 121 & 36 & 66\\ \sum & 195 & 68 & 3297 & 454 & 1163\\\hline \end{matrix}$