Conversión de Unidades y Magnitudes Físicas Fundamentales
En la mayoría de situaciones y por causa de diversas cantidades con unidades diferentes, se requiere convertir la medición de una unidad en otra, por lo que mencionamos algunos pasos que nos facilitarán el proceso de conversión.
- Primero, debemos escribir la cantidad que deseamos convertir, lo podemos representar para mayor entendimiento por medio de un Diagrama. (Más adelante se ejemplifica).
- Se tienen que definir las unidades a convertir en las unidades requeridas.
- Los factores de conversión tienen que ser recíprocos, uno del otro, por lo que siempre existirán dos factores.
- Se multiplicarán las cantidades a convertir por los otros factores (Tanto Numeradores como Denominadores).
- Se dividen los resultados dados en el paso anterior.
- Y por último, se eliminan las unidades, quedando solamente las deseadas.
En mecánica, siendo una de las áreas principales de la Física, se utilizan ciertas Magnitudes Fundamentales que son indispensables para la mayor parte de las aplicaciones.
Empezaremos a estudiar cada una de éstas magnitudes, con sus ejemplos para mayor comprensión.
MAGNITUDES FÍSICAS FUNDAMENTALES
Desde las Sociedades Primitivas el hombre siempre tuvo la necesidad de medir, por lo que utilizaban partes del cuerpo humano como la pulgada, palmada, pie, brazada; pero a medida que se daba el intercambio económico entre los pueblos, se presentaba el problema de no coincidir con los mismos patrones de medición, viéndose afectados y obligados a la necesidad de crear un Sistema Internacional de Unidades.
El Sistema Internacional de Unidades conocido por sus Siglas (SI) parte de las siguientes Magnitudes Fundamentales:
- La Longitud.
- La Masa.
- El Tiempo.
- La Carga Eléctrica.
También detallamos un Sistema de Unidades para cada una de las Magnitudes:
- Sistema M.K.S = Metro, Kilogramo, Segundo.
- Sistema C.G.S = Centímetros, Gramos y Segundo.
- Sistema Inglés = Pie, Libras, Masa, Segundo.
- Sistema Técnico = Metro, UTM (Unidad Técnica de Masa), Segundo.
Ahora estudiaremos cada uno de las magnitudes con sus respectivos sistemas, aplicando ejercicios de conversión.
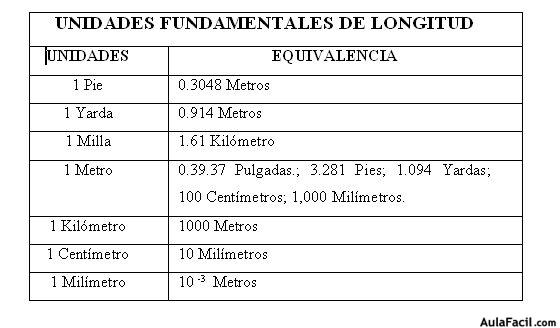
Unidades Fundamentales de Longitud
La Longitud como Magnitud Física se puede expresar por medio de ciertas unidades, las cuáles poseen sus respectivas equivalencias, describiremos algunas que nos facilitarán a la realización de los ejercicios de conversión.
Ejemplos:
a) Convertir 2593 Pies a Yardas.
1. Antes de empezar, es necesario aclarar que algunas equivalencias no se encuentran en las unidades que se requieren, por lo que es necesario hacer dos o más conversiones para llegar a las unidades deseadas.
Ahora bien, para simplificarlo, lo trabajaremos como regla de tres representándolo de la siguiente manera:
2. ¿Cómo llegamos a ésta respuesta? Bueno, como se mencionó en el primer paso, empezamos a simplificar por medio de regla de tres, nos damos cuenta que la primera necesario las unidades de pies a metros y por último de metros a yardas, las cuales son las unidades que deseamos.
3. Por medio del Diagrama se van tachando las unidades que no necesitamos hasta llegar las requeridas.
4. Como último paso, se multiplican las cantidades, es decir, los 2593 por la equivalencia 1.094 yardas ambas funcionando como Numeradores; luego multiplicamos 3.281 Pies x 1 Metro, funcionando como Denominadores.
5. Por último dividimos los resultados, el Numerador con el Denominador, es decir el resultado de multiplicar 2593 x 1.094 que es igual a 2836.74 entre el resultado de multiplicar 3.281 Pies x 1 Metro que es 3.281; obteniendo como resultado los 864.59 Yardas.
OJO! En el Diagrama únicamente eliminamos Unidades (pies, metros) no Cantidades, las cantidades se multiplican o se dividen según sea el caso.
Veamos otro ejemplo:
b) Convertir 27,356 Metros a Millas 1. Realizándolo por medio del Diagrama y Regla de Tres nos quedaría así:2. Aplicamos el mismo procedimiento, eliminando unidades hastallegar a las unidades requeridas.3. Luego multiplicamos las cantidades (27,356 x 1) comoNumeradores y (1000 x 1.61) como Denominadores.4. Procedemos a dividir 27,356 ÷ 1,610, obteniendo como respuesta16.99 Millas.👇 Ejercicios de conversaciónes
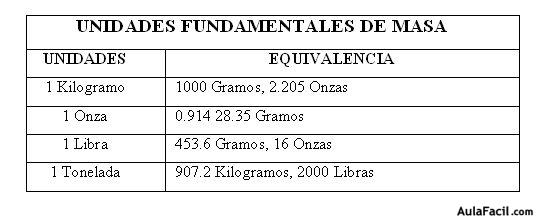
Unidades Fundamentales de Masa y Tiempo
Al igual que las unidades de Longitud, también existen unidades de Masa.Ejemplo:a) Convertir 386 Kilogramos a Libras.
- Cómo en las Conversiones de Longitud, realizamos el mismo procedimiento. Vamos eliminando las unidades, 1 Kilogramo equivale a 1000 Gramos, 1 Libra equivale a 453.6 gramos.
- Luego multiplicamos Numeradores (386 x 1000) = 386,000 y (1 x 453.6)= 453.6.
- Por último dividimos los 386,000 ÷ 453.6, dándonos un resultado de 850.97 Libras.
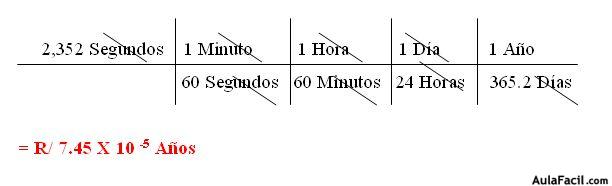
UNIDADES FUNDAMENTALES DE TIEMPOAhora tenemos algunas Unidades de Tiempo:Ejemplo:a) Convertir 2,352 Segundos a Año.En éste caso, las conversiones son más largas, ya que se tienen que convertir los segundos a minutos, minutos a horas, horas a días y días a años que son las unidades que necesitamos.
- Detallamos las Unidades con sus respectivas Equivalencias.
- Ahora multiplicamos los Numeradores (2,352 x 1 x 1 x 1 x 1) = 2,352.
- Luego los Denominadores (60 x 60 x 24 x 365.2) = 31, 553,280
- Ahora dividimos 2, 352 ÷ 48,833,80
- Obteniendo como resultado
La respuesta es un poco diferente, pero aún así siempre se puede hacer uso de la Notación Científica.
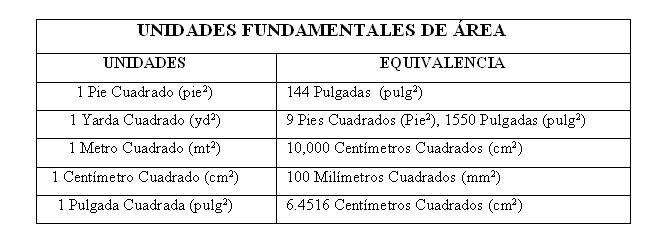
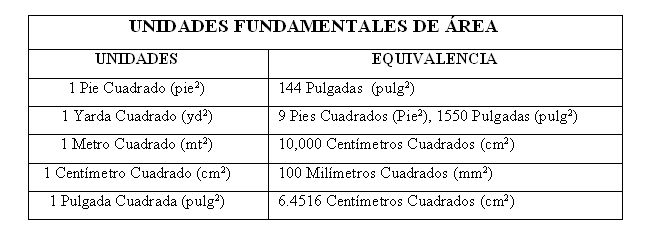
Factores de Conversión para Área y Volumen
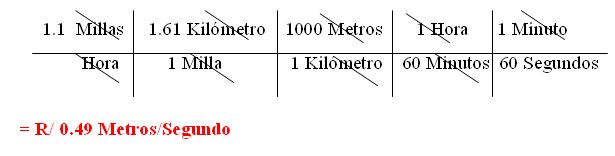
Cómo en las demás magnitudes, también tenemos unidades para Área, para mejor conocimiento las detallamos a continuación:Ejemplo:a) Convertir 1.1 millas/ hora a metros/ segundo.1. Empezamos dibujando el Diagrama para guiarnos mejor.2. Si nos damos cuenta las Unidades están divididas, es decir (Millas/Horas) por lo que tenemos que eliminar Unidades tanto como Nominadores como en Denominadores.3. Siguiendo el mismo procedimiento realizamos las conversiones necesarias hasta llegar a las que deseamos.4. Multiplicamos las cantidades de los Numeradores nos da un resultado de 1771 y en los Denomidadores 3600.5. Ahora dividimos los resultados 1771/3600 dándonos como respuesta 0.49 Metros/Segundo.FACTORES DE CONVERSIÓN PARA VOLUMEN.Describimos algunas Unidades de Conversión para Magnitud Volumen.Ejemplo:a) Un motor de un automóvil tiene un desplazamiento del émbolo de 1595cm y un diámetro del cilindro de 83Mm. Expresar éstas medidas en Pulgadas Cúbicas y en Pulgadas.1. Éste problema es diferente, pero siempre empezamos dibujando el Diagrama como guía.2. En éste caso primero convertimos los 1595cm3. en Pulgadas cúbicas.3. Eliminamos las unidades y hacemos las respectivas conversiones para empezar a multiplicar.Dividimos respuestas (86,405,616/1000,000)4. Nos da una respuesta de 86.40Pulg35. Ahora pasamos los 83mm a pulgadas.
Conversión de Grados a Minutos y Segundos
Para la Conversión de Grados a Minutos, Segundos y Radianes es necesario definir lo que es la Trigonometría.TRIGONOMETRÍA: Es la rama de la Matemática que estudia las propiedades y medidas de ángulos y triángulos.Para ello, es necesario apoyarnos con el Instrumento de la Calculadora y saber algunas unidades de conversión, por ejemplo:1° = 60 Minutos ( 60 ')1 ' = 60 Segundos ( 60 '')Radianes = 180° ( El símbolo de Pi, utilizado en Matemática, tiene un valor numérico de 3.1415927 aproximadamente de 3.1416En una Calculadora Científica, podemos ver ciertas abreviaturas que nos ayudarán a la conversión de las Funciones Trigonométricas, como por ejemplo:
- Grados: (D) (DEG)
- Radianes: (R) (RAD)
- Gradianes: (G) (GRAD)
Ahora veamos un ejemplo.a) Convertir 18.4567 ° a Grados, Minutos y Segundos.1. Como primer paso, tenemos que el número entero es de 18, éste nos equivale a 18°.2. Luego los decimales después del punto es necesario que los pasemos a minutos, así:OJO! Eliminamos unidades iguales y dejamos únicamente la que nos interesa, es decir, los minutos.3. Ahora, tomamos los decimales 402 y los pasamos a Segundos. 0.402 ' x 60 '' (Segundos) = 24.12''4. Ahora unimos todas las respuestas quedándonos 18 ° 27' 24'', que se lee: 18 Grados, 27 Minutos y 24 SegundosNOTA: Si nos damos cuenta en cada conversión trabajamos sólo con los decimales, manteniéndose únicamente el primer número entero que corresponde a los Grados.Veamos otro ejemplo a la inversa.b) Convertir 18° 27' 24'' a Grados1. En éste caso ya no son de Grados a Radianes, sino lo contrario, lo haremos llegar de Segundos, Minutos a Grados. Convertimos los Segundos a Minutos:2. Ahora los 27 Minutos le adicionamos éstos 0.4 minutos y lo convertimos en Grados.3. Sumamos las Unidades Equivalentes, es decir, los 0.456 ° + la cantidad entera 18° quedándonos como respuesta 18.456 °Conversión de Radianes a Grados y Grados a Radianes
👇
Convertir unidades





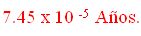


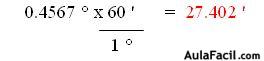
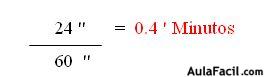
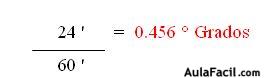
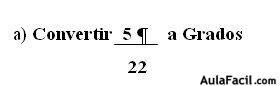
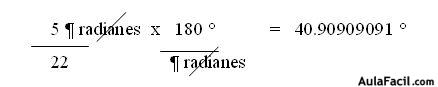
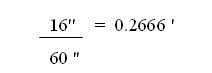
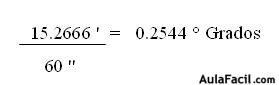
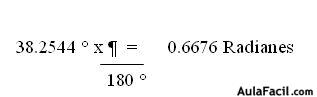
No hay comentarios.:
Publicar un comentario