Introducción
Comentaremos un par de ejemplos para comprender la necesidad y las razones de las conversiones entre las unidades de medida:
En la astronomía, las distancias son extremadamente grandes.
Por ejemplo, tan sólo la distancia del Sol a la Tierra es de unos
150 000 000 kilómetros.
Y el diámetro del supercúmulo de Virgo es de unos
1 892 146 200 000 000 000 000 kilómetros.
En la química nuclear, la distancia media entre dos núcleos de carbono es aproximadamente
0.000000000154 metros.
Es comprensible que trabajar con números tan grandes (o tan pequeños) sea tedioso, a parte de que se necesita más espacio y es fácil equivocarse con alguna de las cifras.
Básicamente, por estas razones, para cada magnitud (longitud, área, volumen, intensidad...) tenemos varias unidades que son múltiplos (o submúltiplos) de la unidad básica (la del SI).
Por ejemplo, podremos decir
10 kilómetros (10 km) en lugar de 10 mil metros (10000 m); ó
3 horas (3 h) en lugar de 10800 segundos (10800 s).
1. Conceptos Básicos
Magnitud, medición, unidad de medida, Sistema Internacional de Unidades (SI)...

Una magnitud es una propiedad física que puede ser medida.
Ejemplos:
Longitud
Tiempo
Temperatura
Volumen
Intensidad de corriente
Una unidad de medida es una cantidad fija que nos permite comparar (medir) una magnitud física indicando a cuántos múltiplos o submúltiplos de esta medida fija equivale.
Una medición es una comparación de una misma magnitud con respecto a la unidad de medida de dicha magnitud.
Ejemplo:
Decimos que una medición es una comparación porque, por ejemplo, cuando decimos que una carretera mide 4 kilómetros de largo, estamos diciendo que la longitud de la carretera es 4 veces la cantidad fija de 1 kilómetro.
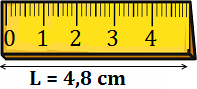
La cantidad fija de 1 kilómetro está indicada en la regla:

Ahora comparamos la longitud de la carretera con la de la regla:
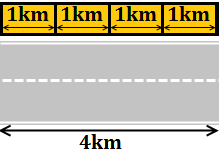
Estamos comparando (midiendo) la longitud de la carretera con la cantidad fija de longitud 1 kilómetro (unidad de medida 1 kilómetro).
Recordad el funcionamiento de las balanzas: para calcular la masa de un objeto realizamos una comparación con un contrapeso hasta alcanzar el equilibrio.

Ejemplos de Unidades de Medida:
Unidades de Longitud: metros, kilómetros, años luz...
Unidades de Tiempo: segundos, minutos, años...
Unidades de Temperatura: grados Celsius, grados Kelvin, grados Fahrenheit...
Unidades de Volumen: metros cúbicos, litros...
Unidades de Intensidad de corriente: amperios
El Sistema Internacional de Unidades (SI) determina las cantidades fijas de 7 magnitudes físicas (longitud, temperatura, tiempo, intensidad luminosa, masa, cantidad de sustancia y corriente eléctrica) y sus unidades de medida.
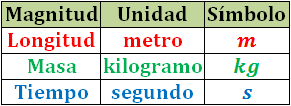
Ahora vamos a ver cómo pasar de una unidad de medida a otra. Por ejemplo, de metros a kilómetros o de metros cúbicos a litros.
La regla que emplearemos para cambiar de unidades es:
«Multiplicar para Bajar
y
Dividir para Subir»
2. Unidades de Longitud (metros)
La escala de las unidades de longitud es
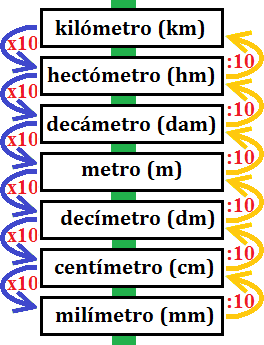
Para cambiar de unidades tenemos que multiplicar por 10 cada vez que bajamos un escalón y dividir entre 10 cada vez que subimos un escalón.
Ejemplo:
Vamos a pasar 2,3 hectómetros a decímetros:
Como vamos a bajar escalones, tenemos que multiplicar por 10 cada vez.
Primer escalón: de hectómetros a decámetros
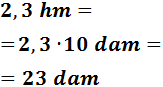
Segundo escalón: de decámetros a metros
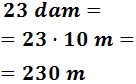
Tercer escalón: de metros a decímetros
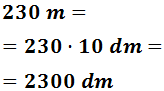
Por tanto, 2,3 hectómetros son 2300 decímetros:
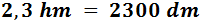
Nota: podemos recorrer varios escalones a la vez multiplicando por una potencia de 10. La potencia es 10 elevado al número de escalones que queremos bajar.
Ejemplo:
Vamos a pasar 2,3 hectómetros a decímetros con una sola operación:
Para pasar de hectómetros a decímetros tenemos que bajar 3 escalones. Por tanto, multiplicamos por 103 = 1000:
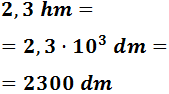
Para subir, dividimos entre 10 elevado al número de escalones que queremos subir. Esta operación es la misma que multiplicar por 10 elevado al número de escalones que queremos subir pero con el exponente en negativo.
Ejemplo:
De 1000 centímetros a metros:
Para pasar 1000 centímetros a metros tenemos que subir dos escalones. Por tanto, multiplicamos por 10-2 = 0,01:
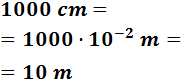
3. Unidades de Área (metros cuadrados)

Recordamos al lector que cuando calculamos áreas empleamos unidades al cuadrado. Por ejemplo, el área de un cuadrado de lado 1 metro es un metro cuadrado, es decir, 1 m2:
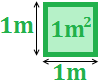
Las unidades para el área son las mismas unidades que para la longitud pero al cuadrado. La escala es
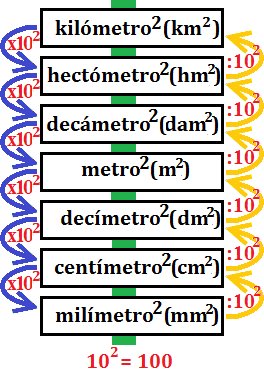
Continuamos con la misma regla:
«Multiplicar para Bajar
y
Dividir para Subir»
Pero tenemos que multiplicar (o dividir) por 100 cada vez que bajamos (o subimos) un escalón.
Ejemplo: vamos a pasar 0,5 kilómetros cuadrados a decámetros cuadrados.
Como tenemos que bajar dos escalones, tenemos que multiplicar dos veces por 100. Esto es lo mismo que multiplicar una vez por 1002:
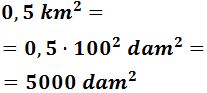
Ejemplo: vamos a pasar 0,5 metros cuadrados a decámetros cuadrados.
Como tenemos que subir dos escalones, tenemos que dividir dos veces entre 100. Esto es lo mismo que dividir una vez por 1002 (o bien, multiplicar por 100-2):
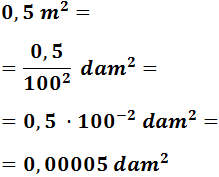
4. Unidades de Volumen (litros)
Recordamos que
El volumen es la magnitud física que expresa el espacio que ocupa un cuerpo en tres dimensiones (ancho, alto y largo).
En el SI la unidad de medida del volumen es el metro cúbico (lo veremos en el apartado siguiente). Ahora vamos a ver la escala de los litros.
Recordamos que aunque estamos acostumbrados a reservar las unidades de los litros para los líquidos, también podemos usarlas para el volumen de cualquier cuerpo, sea sólido, líquido o gaseoso.
Ejemplo: El volumen del interior de una botella de 1L es siempre el mismo, pero podemos llenarla de agua, de arena o de oxígeno. Si la botella es la misma, estas tres sustancias ocuparán el mismo espacio: 1L
Nota: además, si la botella tiene otra forma pero también es de 1L, el espacio es el mismo: 1L.
La escala de los litros es
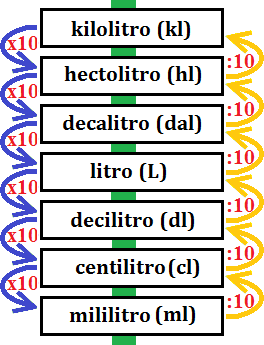
Continuamos con la misma regla:
«Multiplicar para Bajar
y
Dividir para Subir»
Tenemos que multiplicar (o dividir) por 10 cada vez que bajamos (o subimos) un escalón. Es decir, los cálculos son análogos a los que realizamos con la escala del metro (longitud).
Ejemplo: pasamos 2,8 litros a centilitros:
Como tenemos que bajar dos escalones, multiplicamos por 102:
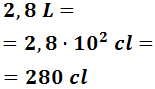
Ejemplo: pasamos de 23 mililitros a decalitros:
Como tenemos que subir cuatro escalones, tenemos que dividir entre 104. Esta operación es la misma que multiplicar por 10-4:
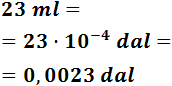
En el siguiente apartado veremos la escala de metros al cubo para referirnos al volumen.
5. Unidades de Volumen (metros cúbicos)
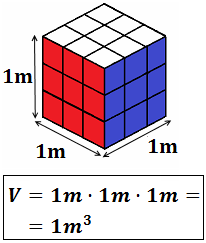
Ya hemos dicho anteriormente que las unidades del volumen pueden ser el litro o los metros cúbicos.
Ejemplo: Si pensamos en un cubo de lado 1m, entonces su volumen es el producto de sus lados:
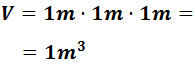
Como vemos, aparece la unidad metros al cubo.
En el siguiente apartado veremos la relación entre las unidades de metros cúbicos y litros.
La escala de los metros cúbicos es
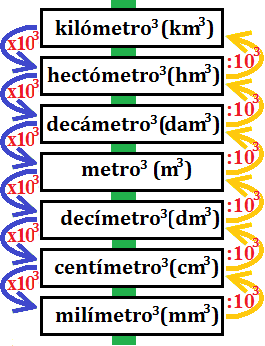
Continuamos con la misma regla:
«Multiplicar para Bajar
y
Dividir para Subir»
Pero tenemos que multiplicar (o dividir) por 103 (diez al cubo) cada vez que bajamos (o subimos) un escalón.
Ejemplo: vamos a pasar 100 milímetros cúbicos a decímetros cúbicos:
Como tenemos que subir dos escalones, tenemos que dividir dos veces por 1000. Esto es lo mismo que dividir una vez por 10002:
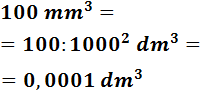
6. De metros cúbicos a litros y viceversa (unidades de volumen)
Calculamos el volumen de un cubo de 10 decímetros de lado:
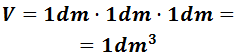
Podemos llenar el cubo de agua:

Pregunta 1: ¿cuánta agua cabe?
La respuesta es fácil: 1 dm3.
Pregunta 2: ¿cuántos litros de agua caben?
Esta segunda pregunta es más difícil de contestar. Los científicos aseguran que
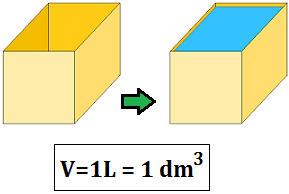
Un decímetro cúbico equivale exactamente al volumen de 1L.
Por tanto, en un decímetro cúbico cabe exactamente 1L de agua.
7. Unidades de Tiempo (segundos)
Las unidades de medida de tiempo son un poco distintas a las demás ya que entre ellas no multiplicamos (o dividimos) siempre por un múltiplo del mismo número.
Por ejemplo, para pasar de horas a minutos tenemos que multiplicar por 60, pero para pasar de días a horas tenemos que multiplicar por 24.
La unidad de tiempo en el Sistema Internacional de Unidades es el segundo, s.
Unidades de Tiempo básicas:
1 minuto = 60 segundos
1 hora = 60 minutos
1 día = 24 horas
1 semana = 7 días
1 mes* = 4 semanas
1 año* = 12 meses
1 lustro = 5 años
1 década = 2 lustros
1 siglo = 10 décadas
1 milenio = 10 siglos
*Nota: algunas unidades no son exactas (mes, año...). Por ejemplo, 1 mes son cuatro semanas, pero puede oscilar entre 28 y 31 días. Esto se debe a que el calendario está basado en los ciclos astronómicos.
Otras unidades de tiempo (agrupaciones de las anteriores):
1 octavario = 8 días
1 trimiestre = 3 meses
1 septenio = 7 años
1 cron = 1 millón de años
También tenemos unidades de tiempo menores que 1 segundo. Estas se asemejan a las escalas anteriores porque son submúltiplos de 10:
10 decisegundos (ds) = 1 segundo
10 centisegundos (cs) = 1 decisegundo
10 milisegundos (ms) = 1 centisegundo
8. Unidades de Masa (gramos)

La masa es la magnitud física que expresa la cantidad de materia de un objeto.
La masa de un objeto no cambia (es constante).
La unidad de medida de la masa es el gramo (g).
Su escala es similar a la de la longitud:
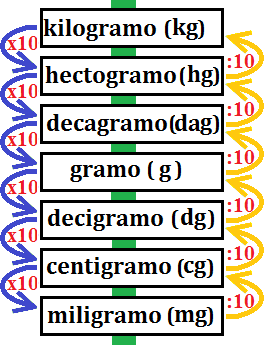
Ejemplo: vamos a pasar 2,3 kilogramos a gramos:
Como tenemos que bajar 3 escalones, multiplicamos 3 veces por 10.
Para hacerlo de un solo paso, multiplicamos por 103:
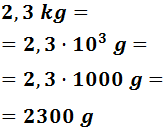
No hay que confundir la masa con el peso:
El peso de un objeto es la fuerza (cuya unidad de medida es el newton) que ejerce la gravedad sobre un objeto:
siendo m la masa del objeto y g la gravedad.
PROBLEMAS DE CONVERSIONES
Problema 1: unidades de longitud
Escribir las siguientes distancias en metros:
15 km
200 dm
23 mm
0,02 dam
2 cm
Antes de empezar, recordamos que la escala es:

Y la frase mnemotécnica:
«Multiplicar para Bajar
y
Dividir para Subir»
15 km
Para pasar de kilómetros a metros tenemos que bajar 3 escalones. Por tanto, multiplicamos tres veces por 10:
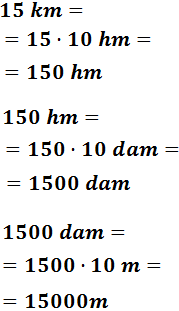
200 dm
Para pasar de decímetros a metros tenemos que subir 1 escalón, por tanto, dividimos una vez entre 10:
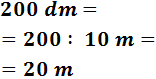
23 mm
Para pasar de milímetros a metros tenemos que subir 3 escalones, por tanto, dividimos tres veces entre 10:
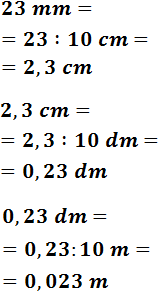
En vez de dividir tres veces entre 10, también podemos dividir una vez entre 1000.
0,02 dam
Para pasar de decámetros a metros tenemos que bajar 1 escalón, por tanto, multiplicamos una vez por 10:
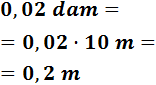
2 cm
Para pasar de centímetros a metros tenemos que subir 2 escalones, por tanto, dividimos dos veces entre 10:
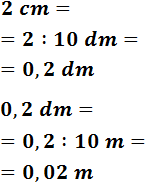
Problema 2: unidades de longitud
Escribir las siguientes longitudes en decámetros realizando un solo paso (multiplicando/dividiendo sólo una vez):
11 mm
5 hm
0,05 dm
Recordamos la escala métrica:

11 mm
Para pasar de milímetros a decámetros tenemos que subir 4 escalones. Por tanto, tenemos que dividir 4 veces entre 10. Podemos realizar estas 4 divisiones dividiendo una sola vez por 104 = 10000:
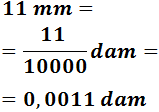
Si queremos evitar los decimales podemos usar notación científica:
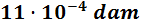
5 hm
Para pasar de hectómetros a decámetros tenemos que bajar un escalón:
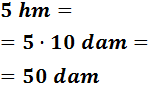
0,05 dm
Para pasar de decímetros a decámetros tenemos que subir dos escalones. Por tanto, dividir dos veces entre 10, que es lo mismo que dividir entre 102 = 100:
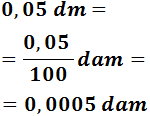
En notación científica:
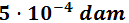
Problema 3: unidades de área
Escribir las siguientes áreas en decímetros cuadrados:
13 mm2
200 dam2
0,0000003 km2
Recordamos la escala de metros cuadrados:

13 mm2
Para pasar de milímetros a decímetros tenemos que subir 2 escalones.
Como estamos trabajando con áreas, tendremos que dividir dos veces entre 102 = 100:
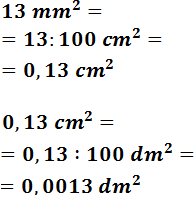
En notación científica:
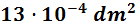
200 dam2
Para pasar de decámetros a decímetros tenemos que bajar (multiplicar) 2 escalones.
Multiplicamos 2 veces por 100:
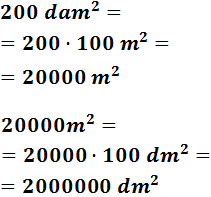
En notación científica:
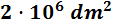
0,0000003 km2
Para pasar de kilómetros a decímetros tenemos que bajar 4 escalones.
Por tanto, multiplicamos 4 veces por 100:
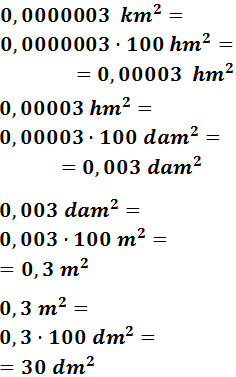
Problema 4: unidades de área
Escribir las siguientes áreas en kilómetros cuadrados multiplicando o dividiendo sólo una vez:
1,3 dam2
0,12 hm2
5 mm2
Recordamos la escala de metros cuadrados:

1,3 dam2
Para pasar de decámetros a kilómetros tenemos que subir 2 escalones. Por tanto, tenemos que dividir dos veces entre 100.
Dividir dos veces entre 100 es lo mismo que dividir una vez entre 10000:
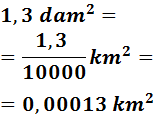
En notación científica:
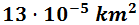
0,12 hm2
Como tenemos que subir 1 escalón, dividimos una vez entre 100:
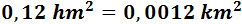
En notación científica:
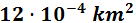
5 mm2
Tenemos que subir 6 escalones, lo que supone dividir 6 veces entre 100. Esto es lo mismo que dividir una vez entre 1006.
Además, notemos que podemos escribir
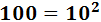
De este modo,
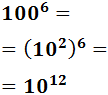
Escribimos directamente en notación científica porque tenemos demasiados ceros:
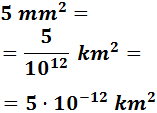
Problema 5: unidades de volumen
Escribir las siguientes medidas en litros:
2,3 ml
4,1 kl
2 dal
3 m3
0,005 km3
9 mm3
La escala de los litros es:

2,3 ml
Para pasar de mililitros a litros tenemos que subir 3 escalones:
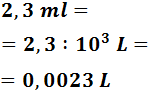
En notación científica:
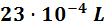
4,1 kl
Para pasar de kilolitros a litros tenemos que bajar 3 escalones:
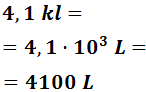
2 dal
Para pasar de decalitros a litros tenemos que bajar 1 escalón:
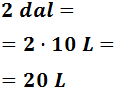
3 m3
Como tenemos el volumen en metros cúbicos, tendremos que usar la relación
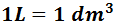
Pasamos a decímetros cúbicos (bajamos 1 escalón) y ya tendremos las unidades en litros:
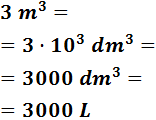
0,005 km3
Bajamos 4 escalones:
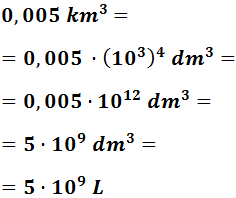
9 mm3
Subimos 2 escalones:
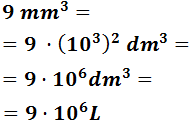
Problema 6: unidades de tiempo
Escribir las siguientes medidas en minutos:
3 horas
2 días
2 meses
1980 segundos
3 horas
Para pasar de horas a minutos tenemos que multiplicar por 60:
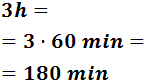
2 días
Un día son 24 horas y una hora son 60 minutos:
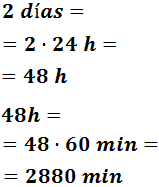
2 meses
Un mes son 4 semanas; 1 semana son 7 días; 1 día son 24 horas; y 1 hora son 60 minutos:
Multiplicamos por 4 para pasar de meses a semanas:
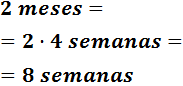
Multiplicamos 7 para pasar de semanas a días

Multiplicamos por 24 para pasar de días a horas
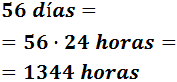
Multiplicamos por 60 para pasar de horas a minutos
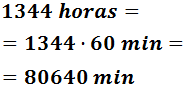
1980 segundos
Un minuto son 60 segundos. Por tanto, para pasar de segundos a minutos tenemos que dividir entre 60:
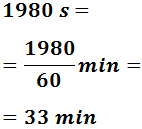
Problema 7: unidades de tiempo
Escribir los siguientes tiempos en días:
Un año y medio
2 trimestres
Un sexenio
Dos octavarios
259200 segundos
1440 minutos
Un año y medio
Un año son 365 días y, por tanto, un año y medio son
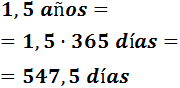
2 trimestres
1 trimestre son 3 meses; un mes son 28 días.
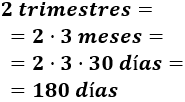
Un sexenio
Un sexenio son 6 años.
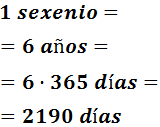
Dos octavarios
Un octavario son 8 días.
Por tanto, dos octavarios son 16 días.
259200 segundos
Pasamos a minutos:
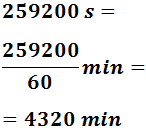
Pasamos a horas:
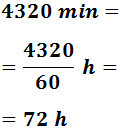
Pasamos a días:
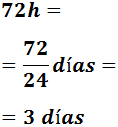
1440 minutos
Pasamos a horas y después a días dividiendo entre 60 y entre 24:
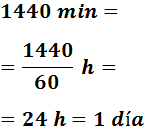
Problema 8
Calcular cuántos litros de agua caben en una piscina de dimensiones 3x6x23 m.
Las dimensiones son las longitudes del ancho, largo y profundidad.
Podemos escribir las dimensiones en decímetros:
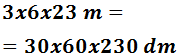
Por tanto, el volumen de la piscina es
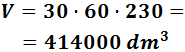
Y como tenemos las unidades en decímetros cúbicos, tenemos los litros:
Problema 9
Calcular los litros de agua que caben en un recipiente esférico de cristal de radio 0,2 metros.

Ayuda: el volumen de una esfera es
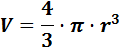
siendo r el radio.
El radio es 0,2 metros, es decir, 2 dm.
Sabemos que el volumen de una esfera es
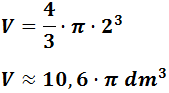
Aproximando π = 3,14159 :
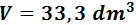
El volumen lo tenemos en decímetros cúbicos porque hemos escrito el radio en decímetros.
Por tanto, se necesitan, aproximadamente 33,3 L (porque 1L = 1dm3).
Problema 10
Calcular la masa total de un bidón metálico de 1kg con forma cilíndrica de 1 metro de radio y 2 metros de altura lleno de agua.
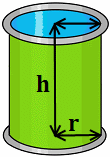
Ayuda: 1L de agua es 1kg de agua.
Las medidas del cilindro son 10 decímetros de radio y 20 decímetros de altura.
El área de la base es
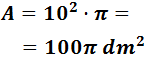
Por tanto, el volumen del cilindro es (área de la base por la altura)
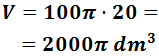
Podemos aproximar con π = 3,14159:
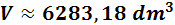
Por tanto, como 1dm3 es 1L y 1L es un 1kg, la masa del agua es, aproximadamente, 6283,18kg.
Por tanto, la masa total del bidón (con agua) es
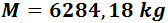
No hay comentarios.:
Publicar un comentario