Función racional

Funciones racionales
Funciones exponenciales
Funciones logaritmica

En este artículo te voy a explicar brevemente lo que son las funciones racionales y te mostraré unas funciones racionales ejemplos para que las entiendas mejor.Una función es racional si: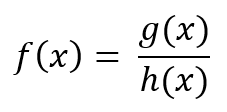en donde g(x) y h(x) son polinomios. El dominio de la función serán todos los números reales con excepción los números en los cuales se hace cero el denominador.

Por ejemplo en una función f (x ) = 1 / x – 2, el dominio es toda x excepto x =2.

Ejercicio explicado de función racional.

Cuando se hace la gráfica de una función racional es importante saber:

• Qué se puede decir de los valores de la función cuando x se acerca a un cero del denominador?
• Qué se puede decir de los valores de la función cuando x es grande y positiva o negativa?

Asíntota vertical

La recta x = a es una asíntota vertical de la gráfica de una función si f (x) –> ∞ o f (x) –> -∞ cuando xtiende a a.

Asíntota horizontal

La recta y = c es una asíntota horizontal de la gráfica de una función si f (x) –> c cuando x –> ∞ o cuando x  –> -∞ 

Funciones racionales EJEMPLOS

En los siguientes ejemplos graficaremos cada función racional. Recuerda que puedes hacer las gráficas por medio de una tabla de valores en donde seleccionas valores de x y sustituyes en la función (ese será el valor de y).

 1. f (x) = 3 / (x – 4)2. f (x) = -3x / (x + 2)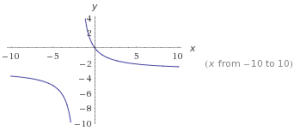3. f (x) = (x -2) / (x2 – x – 6)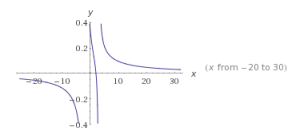

Graficando funciones racionales

Las funciones racionales son de la forma y = f ( x ), donde f ( x ) es una expresión racional .

Algunos de los ejemplos de funciones racionales son:

 ,  , 

Las gráficas de las funciones racionales pueden ser difíciles de dibujar. Para dibujar una gráfica de una función racional, puede comenzar encontrando lasasíntotas y las intercepciones.

Pasos involucrados para graficar las funciones racionales:

1. Encuentre las asíntotas de la función racional, si las hay.
2. Dibuje las asíntotas como rectas punteadas.
3. Encuentre la intercepción en x y la intercepción eny de la función racional, si las hay.
4. Encuentre los valores de y para varios valores diferentes de x .
5. Grafique los puntos y dibuje una curva lisa que conecte los puntos. Asegúrese que la gráfica no cruce las asíntotas verticales.

Ejemplo:

Grafique la función racional

La asíntota vertical de una función racional es el valor de x donde el denominador de la función es cero. Iguale el denominador a cero y encuentre el valor de x .

2 x + 1 = 0

x = -1/2

La asíntota vertical de la función racional es x = -0.5.

Esta función tiene la intercepción en x en (-1/4, 0) y la intercepción en y en (0, 1). Encuentre más puntos en la función y grafique la función.

Algunas veces la función racional dada tiene que ser simplificada, antes de graficarla. En ese caso, si hay algunos valores excluidos (donde la función no esté definida) diferentes de las asíntotas, entonces hay un paso adicional involucrado al graficar la función.

Para representar la función no definida, asegúrese que la función no es una curva lisa continua en el valor excluido. Este valor excluido es usualmente referido como un hoyo en la función racional.

Por ejemplo, la función racional  tiene un hoyo en x = 0.

COMO CALCULAR LAS ASINTOTAS DE UNA FUNCION RACIONAL

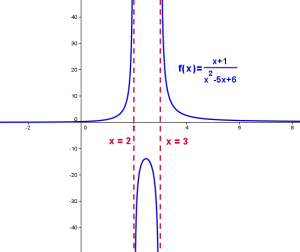
Asíntotas Verticales (A.V.)

Para encontrar las asíntotas verticales, igualamos el denominador a cero, y encontramos las soluciones o ceros.  En el video que viene líneas abajo, veremos a detalle como encontrar las asíntotas verticales.

Aquí viene la gráfica de una función con asíntota vertical.

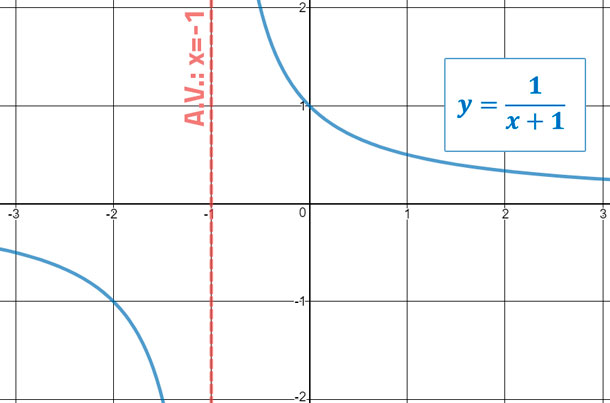
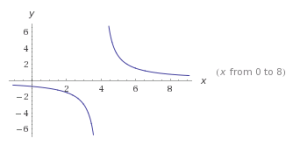
Asíntotas Horizontales (A.H.)

Para encontrar las asíntotas horizontales, necesitamos comparar el grado del numerador(GN) y con el grado del denominador (GD).

Donde, CPN es el coeficiente principal del numerador; y CPD es el coeficiente principal del denominador.

Aquí viene la gráfica de una función con asíntota horizontal.

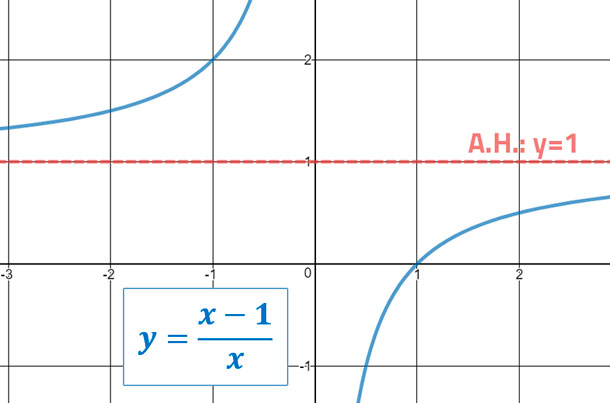
Asíntotas Oblicuas (A.O.)

Solo hay asíntota oblicua o diagonal, si es que no hay asíntotas horizontales y  GN – GD = 1.

La asíntota oblicua es el cociente de la división entre P(x) y Q(x).

Veamos la gráfica de una función con asíntota oblicua:

Hallar, si existen, las asíntotas oblicuas de la función:

En primer lugar descartamos que existan asíntotas horizontales (incompatibles con las oblicuas):

El límite es infinito, por lo que no existen asíntotas horizontales. Podemos ver el parámetro p (pendiente) de la recta de la posible asíntota oblicua mediante el valor del límite:

Como el límite tiene un valor finito y ≠ 0, p = 1, existe una asíntota oblicua.

Se averigua ahora el punto q, de corte con el eje Y, mediante este límite:

La ecuación de la asíntota oblicua, de pendiente positiva, de esta función es:

Como se ve en la figura:

Ejemplo 2

Hallar, por el procedimiento descrito en esta página, las ecuaciones de la hipérbola que aparece en el ejercicio de la página de Universo Fórmulas asíntotas de una hipérbola.

En este ejercicio, los parámetros de la hipérbola son a = 2 y b = 4.

La ecuación de la hipérbola será:

De la que despejamos la y:

Mediante el límite siguiente se descartan las asíntotas horizontales, para que puedan existir las oblicuas:

No hay asíntotas horizontales, porque el límite es infinito. Vamos a ver la pendiente p de la/las asíntotas oblicua/s:

Porque es el límite de una razón polinómica con el mismo orden en el numerador y el denominador.

Existen dos asíntotas oblicuas porque los valores de sus pendientes p ± 0. Hallaremos el punto q de intersección con el eje Y:

El valor de este límite (de q) es 0. Se llega a él después de una indeterminación ∞ – ∞ que ya se ha mostrado su resolución en el enlace correspondiente.

Por lo tanto, las ecuaciones de las asíntotas oblicuas buscadas son:

Se ha llegado al mismo resultado que en el ejercicio de la página de Universo Formulas asíntotas de una hipérbola.

EJERCICIOS A RESOLVER