Un vector es un ente matemático, como el punto, la recto o el plano. Un vector se representa mediante un segmento de recta orientado (una flecha), y tiene siempre 3 elementos muy importantes: módulo, dirección y sentido. Veamos otros detalles y también, algunos ejercicios resueltos.
Un vector se representa mediante una letra con una flechita sobre ella, por ejemplo, aquí tenemos al vector A:

Elementos del vector
El vector siempre tendrá 3 elementos: módulo, dirección y sentido.
i) Módulo
Es el tamaño o longitud del vector y hace referencia a la intensidad de la magnitud que representa. Para indicar el módulo de un vector, colocamos el vector dentro de 2 barras.
Por ejemplo, aquí tenemos al módulo del vector A, que se representa como el vector A dentro de 2 barras.

ii) Dirección
Es la línea de acción del vector. Su orientación en el plano cartesiano se define mediante el ángulo que forma el vector con el semieje x positivo en posición normal. A este ángulo, lo llamaremos θ (theta).
Por ejemplo, la dirección del vector A, se define por el ángulo θ que es igual a 37°.

iii) Sentido
Se representa gráficamente por una cabeza de flecha. Indica hacia que lado de la dirección o línea de acción actúa el vector.
Por ejemplo, aquí vemos el sentido del vector A.

¿Para qué sirven los vectores?
Seguramente pensarás que nunca en tu vida has visto un vector y que no tienen mucha utilidad, sin embargo, los vectores nos permiten representar magnitudes vectoriales. ¿Y qué es eso?
Magnitudes
Recordemos que una magnitud es todo aquello que se puede medir. Por ejemplo, mi lapicero tiene una longitud de 17 centímetros.
De acuerdo a su naturaleza, las magnitudes se clasifican en escalares y vectoriales.
Magnitudes escalares: son aquellas que quedan completamente definidas con un número seguido de una unidad. Son magnitudes escalares: longitud, masa, tiempo, trabajo, densidad, potencia, energía, carga eléctrica, potencial eléctrico.
Por ejemplo, en mi ciudad, la temperatura es de 38°C …. Temperatura = 38°C.
La duración de un video de MateMovil, suele ser de 15 minutos … Tiempo = 15 minutos.
La duración de un video de MateMovil, suele ser de 15 minutos … Tiempo = 15 minutos.
Magnitudes vectoriales: son aquellas que se definen mediante su módulo, pero además también es necesario conocer su dirección y sentido que esté plenamente definida. Son magnitudes vectoriales: desplazamiento, velocidad, aceleración, fuerza, torque, impulso, cantidad de movimiento, intensidad de campo eléctrico, inducción magnética.
Los vectores nos permiten representar las magnitudes vectoriales, y con ello, muchos fenómenos naturales.
Ejemplos prácticos: la velocidad de un avión, o la fuerza de una resortera.
¿Cómo se calcula el módulo de un vector?
Para calcular el módulo de un vector, usaremos la siguiente fórmula:

Ejemplo:
Calcular el módulo del vector A a partir de la gráfica:
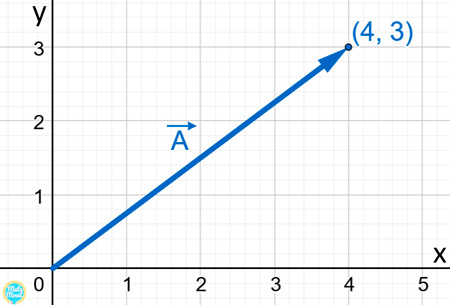
Solución:
Para calcular el módulo del vector A, solo tenemos que trabajar con sus componentes en «x» e «y», y usar la fórmula del módulo que vimos líneas arriba.

¿Cómo se calcula la dirección de un vector?
La dirección de un vector, se define mediante el ángulo θ, usando la siguiente expresión:
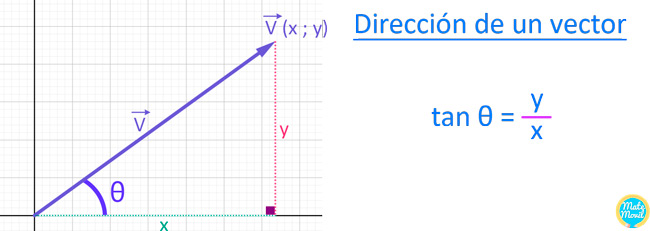
Ejemplo:
Calcular la dirección del vector A, a partir del gráfico:

Solución:
La dirección o línea de acción define mediante el ángulo θ, y para calcular el valor de ese ángulo, usaremos la fórmula que vimos líneas arriba.
Además, nos será de mucha utilidad la tabla de razones trigonométricas de ángulos notables.

Ahora aplicamos la fórmula:

Nota: el triángulo 37°-53°, es un triángulo notable aproximado, por ello, colocamos que θ, es aproximadamente igual a 37°.
Guía de ejercicios
A continuación, viene una guía con muchos ejercicios de vectores, resolveremos algunos en el video que viene líneas abajo.

No hay comentarios.:
Publicar un comentario